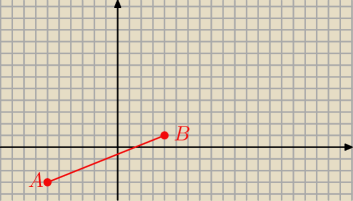
geometria analityczna Karol: dane są punkty A(−6,−3) i B(4,1). Wyznacz współrzędne punktu C leżącego na Osi Y tak aby pole trójkąta było równe 13

janek191: I AB I = 2 √29

	13
P = 0,5 *2√29*h = √29*h = 13 ⇒ h =
	√29

C = ( 0, y) Odległość C od pr AB = h Dokończ

chichi: Pole trójkąta z użyciem wyznacznika, gdzie C = (0, y). Otrzymasz rownanie z jedną zmienną

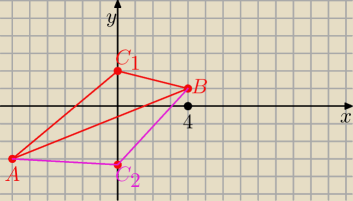
janek191: C₁ = ( 0, 2) C₂ = ( 0; − 3,2)

Karol: nie wiem jak wyliczyc...

Karol:

	2		3
równanie prostej jest		x−y−		=0
	5		5

janek191: Pomnóż obustronnie przez 5. 2 x − 5 y − 3 = 0

janek191:

	I 2*0 − 5*y − 3 I		13
Mamy		=
	√22 + (−5)2		√29

Karol: Wyszedł mi 0,2

Karol: a jak wyliczyc c2?

chichi: Przecież moduł doprowadza do dwóch możliwych wyników na współrzędną punktu C...

janek191: I − 5 y − 3 I = 13 − 5 y −3 = − 13 lub − 5 y − 3 = 13 − 5 y = − 10 lub −5y = 16

	16
y = 2 lub y = −		= − 3,2
	5