trójkąt równoboczny
Paulinka: Dane są dwa wierzchołki trójkąta równobocznego A(1;2) i B(5;2).
Znajdz: a) wierzchołek C b) pole trójkąta
29 paź 10:26
wredulus_pospolitus:
(a)
krok 1: wyznaczamy połowę odcinka AB (oznaczmy jako punkt D)
krok 2: wyznaczamy długość odcinka AB
krok 3: wyznaczamy prostą prostopadłą do odcinka AB zaczepioną w punkcie D
| | √3 | |
krok 4: wyznaczamy punkty C i C' leżące na wyznaczonej prostej oddalone o |
| |AB| |
| | 2 | |
(b)
krok 2 z (a) −−−> wstawiamy do wzoru na pole trójkąta równobocznego
29 paź 10:47
wredulus_pospolitus:
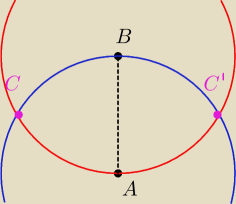
sposób drugi do (a):
krok 1: wyznaczamy długość odcinka AB
krok 2: wyznaczamy wzór okręgu o środku w A i promieniu |AB|
krok 3: wyznaczamy wzór okręgu o środku w B i promieniu |AB|
krok 4: rozwiązujemy układ równań (de facto przyrównujemy do siebie równania) −−− rozwiązaniami
będą współrzędne punktu C i C'
Uwaga ogólna −−− ewentualnie odrzucamy jedno z C lub C' ze względu na 'kolejność oznaczeń
wierzchołków trójkąta'.
29 paź 10:51
pik:
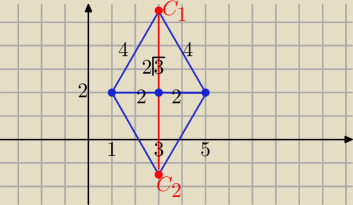
a=4
C
1=(3,2
√3+2)
C
2=(3,2
√3−2)
29 paź 10:52
wredulus_pospolitus:
zał. x∊ (1;5)
(x−1)2 + (y−2)2 = 16
(x−5)2 + (y−2)2 = 16
stąd: (x−1)2 = (x−5)2 −−−> x=3
(3−1)2 + (y−2)2 = 16 −−−> (y−2)2 = 12 −−−> y−2 = ±2√3 −−−> y = 2 ± 2√3
C(3, 2 + 2√3) ; C'(3, 2 − 2√3)
29 paź 10:54
pik:

29 paź 10:55
pik:
rzecz jasna : C
2(3, 2−2
√3)

29 paź 10:59
chichi:
A jak wygląda wzór funkcji dwóch zmiennych C
2?

29 paź 11:44
 sposób drugi do (a):
krok 1: wyznaczamy długość odcinka AB
krok 2: wyznaczamy wzór okręgu o środku w A i promieniu |AB|
krok 3: wyznaczamy wzór okręgu o środku w B i promieniu |AB|
krok 4: rozwiązujemy układ równań (de facto przyrównujemy do siebie równania) −−− rozwiązaniami
będą współrzędne punktu C i C'
Uwaga ogólna −−− ewentualnie odrzucamy jedno z C lub C' ze względu na 'kolejność oznaczeń
wierzchołków trójkąta'.
sposób drugi do (a):
krok 1: wyznaczamy długość odcinka AB
krok 2: wyznaczamy wzór okręgu o środku w A i promieniu |AB|
krok 3: wyznaczamy wzór okręgu o środku w B i promieniu |AB|
krok 4: rozwiązujemy układ równań (de facto przyrównujemy do siebie równania) −−− rozwiązaniami
będą współrzędne punktu C i C'
Uwaga ogólna −−− ewentualnie odrzucamy jedno z C lub C' ze względu na 'kolejność oznaczeń
wierzchołków trójkąta'.
 a=4
a=4


