Pc i V ostrosłupa Milenka: Długość każdej krawędzi ostrosłupa prawidłowego czworokątnego jest równa 6 cm. Oblicz pole całkowite i objętość tej bryły.

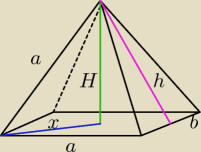
Łukasz: a=6 cm Do obliczenia objętości potrzebna jest wysokość H i pole podstawy

	1		1
x=		a√2=		*6√2=3√2 − połowa przekątnej kwadratu
	2		2

Z twierdzenia Pitagorasa H²+x²=a² H²=36−18 H=√18=3√2

	1
V=		Pp*H
	3

	1		1
V=		*a2*H=		*62*3√2=36√2 cm3
	3		3

Pole powierzchni niedługo chyba że ktoś mnie uprzedzi

Łukasz: Pole powierzchni składa się z 4 trójkątów równobocznych o boku a i kwadratu o boku a, więc

	a2√3		62√3
P=a2+4*		=62+4*		=(36+36√3)cm2
	4		4

Na rysunku wysokość h ściany bocznej można pominąć