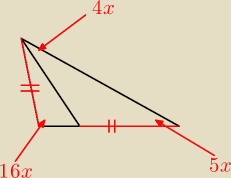
kąty 123: Jak obliczyć x?

janek191: Co oznacza x?

123: to sa katy

janek191: Rozwartość kątów oznaczamy łukami

chichi: No to jak już je oznaczymy łukami, to jaka będzie miara 'x'?

an: sin4xsin16x=sin9xsin5x x=6^o

student: 25x = 180 x = 6

an: po pierwsze skąd 25x = 180 po drugie180/25=7,2

chichi: Po pierwsze skąd to równanie? Po drugie 25 * 6 = 150, nie 180^o

an: Moim zdaniem 4x to kąt z czarnych odcinków, moje równanie wynika z dwukrotnego skorzystania z twierdzenia sinusów

chichi: @an wiem skąd wynika Twoje równanie, ja pisałem do @student. Na pewno tak jest, co sugeruje już sam rysunek, równość odpowiednich boków itd. Bo co by to wnosiło do zadania jeśli mielibyśmy 3 kąty w trójkącie uzależnione od jednej zmiennej...

student: no suma kątów to 25x suma kątów w trojkącie to 180 stopni więc 25x = 180

chichi: Ten kąt 4x przy górnym wierzchołku to kąt pomiędzy tymi czarnymi bokami, a nie czarnym a czerwonym

an: @student to zadanie byłoby banalne, mało tego w ramach ćwiczenia spróbuj narysować taki trójkąt pokaż jak on wygląda.

chichi: Mało tego, po co byłby ten odcinek łączy górny wierzchołek z tym dolnym bokiem, malo tego po co zaznaczona byłaby na rysunku równość odpowiednich boków, dziś nie 1 kwietnia

chichi: Później wrzucę rozwiązanie bez 'strzelania'

Mariusz: @student an najprawdopodobniej dwukrotnie skorzystał z twierdzenia sinusów i dlatego otrzymał taki wynik

chichi: @Mariusz "moje równanie wynika z dwukrotnego skorzystania z twierdzenia sinusów" tak, wspomniał o tym, próbowałeś rozwiązywać to równanie bez strzelania? Bo Ty lubisz się w takie rzeczy bawić, wymaga to nieco pracy

Mariusz: Ja i bez czytania tego wpisu wiedziałem z czego skorzystał Z tej równości iloczynów sinusów można było już wywnioskować czego użył Mamy tutaj jedną parę boków o równej długości i jeden wspólny bok więc da się sensownie ułożyć równania z twierdzenia sinusów

chichi: No pewnie to jest oczywiste, ale napisałeś, że 'najprawdopodobniej' więc napisałem Ci, że na pewno, a nie prawdopodobnie, bo o tym wspomniał

Mariusz:

y		y
	=
sin4x		sin9x

z		z
	=		// z twierdzenia sinusów
sin16x		sin5x

yz		yz
	=
sin4x sin16x		sin9x sin5x

	sin9x sin5x
yz		= yz
	sin4x sin16x

yz sin9x sin5x = yz sin4x sin16x yz (sin9x sin5x − sin4x sin16x)=0 2sin9x sin5x − 2sin4x sin16x = 0 cos(α−β)=cos(α)cos(β)+sin(α)sin(β) cos(α+β)=cos(α)cos(β)−sin(α)sin(β) cos(α−β)−cos(α+β)=2sin(α)sin(β) (cos(4x)−cos(14x))−(cos(−12x)−cos(20x))=0 cos(20x)−cos(14x)−cos(12x)+cos(4x)=0 Teraz wielomiany Czebyszowa byłyby przydatne gdybyśmy chcieli to równanie sprowadzić do równania wielomianowego

an: Rozwiązać to równanie przy pomocy wzorów Eulera być może się uda, ale czy nie istnieje prostszy sposób. Ciekawe czy @student wie dlaczego nie można narysować trójkąta jaki On proponuje.

Mariusz: Można przyjąć 2x = α , wtedy obniżymy stopień równania wielomianowego które dostaniemy po skorzystaniu z wielomianów Czebyszowa cos(10α)−cos(7α)−cos(6α)+cos(2α)=0

Mariusz: an a tak przejście na zespolone to też jakaś opcja ale gdybyśmy chcieli rozwiązywać to równanie korzystając tylko z liczb rzeczywistych to nie przychodzi mi nic innego do głowy jak wielomiany Czebyszowa Na wielomiany Czebyszowa można stosunkowo łatwo wyprowadzić wzór rekurencyjny a wzór jawny można otrzymać chociażby z funkcji tworzącej (tyle że będzie ona dwuargumentowa) cos((n+1)α)=cos(nα)cos(α)−sin(nα)sin(α) cos((n−1)α)=cos(nα)cos(α)+sin(nα)sin(α) cos((n+1)α)+cos((n−1)α)=2cos(α)cos(nα) Niech cos(α)=x Wzór rekurencyjny na wielomiany Czebyszowa wygląda następująco T₀=1 T₁=x T_n+1=2xT_n−T_n−1 Tak jak pisałem wzór jawny można otrzymać chociażby z funkcji tworzącej

Mariusz: Chichi ty pisałeś że masz jakiś ciekawszy sposób bo ten z twierdzeniem sinusów rzeczywiście wymaga trochę obliczeń

Mariusz: Napisałem w C# program do obliczania pierwiastków równań wielomianowych metodą obliczającą wartości własne macierzy stowarzyszonej (Rozkład QR napisałem z wykorzystaniem obrotów Givensa − musiałem rozpisać mnożenie macierzy przez macierze obrotów Givensa bo nigdzie nie znalazłem rozkładu QR wyjaśnionego w sposób przydatny programiście , to co widziałem mogłoby być przydatne jedynie matematykowi , w przypadku odbić Householdera nie miałem pomysłu jak zrealizować ten rozkład macierzy a nie chciałem mnożyć macierzy tylko po to aby uzyskać rozkład QR) Gdyby napisać w C# klasę wielomianów z przeciążonymi operatorami +, −, *, / , % oraz z funkcjami GCD,Horner to można by rozwiązać to zadanie numerycznie

chichi: @Mariusz ja się niestety nie znam na programowaniu i wcale mnie to nie pociąga. To trzeba po prostu lubić

Mariusz: No to jak uda ci się zdobyć co najmniej doktora to pewnie zostaniesz na uczelni Jak nie to pewnie zostaniesz nauczycielem bo nie widzę innych możliwości po matematyce i jeśli nie pociąga cię programowanie

chichi: Albo zrobię porządną gromadkę dzieci i będzie wypłata

Kacper: Ciekawe kto je będzie wychowywał

chichi: Dziadkowie, teściowie i matka