Liczby zespolone anonim123: Jak wykonać zadanie z⁴+1=0 ? Trzeba skorzystać ze wzoru na pierwiastek n tego stopnia z z? Mi wychodzi wtedy dzielenie przez zero co nie może się zdarzyć

ICSP: nie trzeba. z⁴ + 1 = z⁴ + 2z² + 1 − 2z² = (z² − √2z + 1)(z² + √2z + 1) Wystarczy rozwiązać dwa równania kwadratowe.

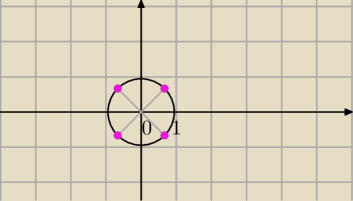
Mila: 1) z⁴=−1 |−1|=1 φ=π

	π+2kπ		π+2kπ
zk=4√1*(cos		+i sin		), dla k∊{0,1,2,3}
	4		4

	π		π		√2		√2
z0=cos		+i sin		=		+i*
	4		4		2		2

	3π		3π		√2		√2
z1=cos		+i sin		=−		+i*
	4		4		2		2

	5π		5π		√2		√2
z2=cos		+i sin		=−		−i*
	4		4		2		2

	7π		7π		√2		√2
z3=cos		+i sin		=		−i*
	4		4		2		2

lub tak: 2 ) z⁴−i²=0 (z²−i)*(z+i)=0 z²=i lub z²=−i⇔

	(1+i)2		(1−i)2
z2=		lub z2=
	2		2

	1+i		1+i		1−i		1−i
z=		lub z=−		lub =		lub z= −
	√2		√2		√2		√2

anonim123: A jak obliczyć kąt fi bo mi tutaj wychodzi dzielenie przez zero?

anonim123: Dziękuję za wcześniejsze odpowiedzi 😄

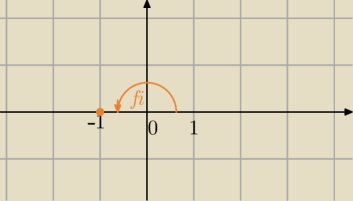
Mila: z=−1+0i cosφ=−1 φ=π gdzie masz dzielenie przez zero, wcale nie liczę , tylko odczytuję z układu wsp.

anonim123: Już to widzę dzięki Mila😄