geometria anlityczna mar: Mam takie zadanie: Oblicz promień okręgu opisanego na trójkącie o wierzchołku A(6,−1) B(−2,3) C(−3,−4). Od razu powiem, że nie jest to trójkąt prostokątny, ani równoramienny. Próbowałem rozwiązać to zadanie za pomocą równania okręgu i wyszło r=5,5.

	abc
Próbowałem też za pomocą wzoru R=		, ale już przy liczeniu samego r poległem, bo mi
	4rp

jakieś straszne pierwiastki wychodzą. Ale bardziej mnie nurtuje pytanie czy jest jeszcze jakiś inny sposób?

chichi:

	abc
Zauważ, że PΔ = rp, zatem R =		, no to jedziemy:
	4P

P_Δ = 3 ∧ |AB| = 2√5 ∧ |BC| = √26 ∧ |AC| = 3√10

	2√5*√26*3√10
⇒ R =		= 5√13
	4*3

chichi: Nie ma co wyznaczać 'r', tylko pole trójkąta, do którego dobieramy się najszybciej w ten sposób: https://www.geogebra.org/m/CIlxpp4u

chichi: A tutaj 'poradnik': https://www.youtube.com/watch?v=IZtiC4o8B9s&ab_channel=PiotrSzlagor W tablicach CKE też znajduje się odpowiedni wzór na stronie 6, on jest właśnie odpowiednio przerobiony, gdyż nie każdy w liceum poznaje pojęcie wyznacznika macierzy

mar: Tak na szybko widzę, że powinno być |AB|=⁴√5, |BC|=5√2, |BC| się zgadza, stąd inne R wyszło (mam taką nadzieję). No tak, wyznacznik macierzy do wyznaczenia pola, o tym zapomniałem. Ale faktycznie PΔ = rp. Nigdy się z tym nie spotkałem. Dzięki

chichi: Ehhh... Ja źle przepisałem punkty, przyjąłem A=(6, −1) B=(2, −3) C=(−3, −4) czyli zamieniły mi się znaki w punkcie B przy przepisywaniu, stąd wyniki będą inne, ale poradzisz sobie sam wzorując się na moim przykładzie, może to i dobrze, że się kopnąłem, bo masz okazję sam rozwiązać zadanie i przećwiczyć

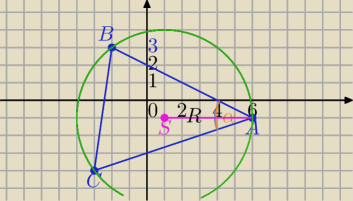
Mila: A=(6,−1), B=(−2,3), C=(−3,−4). 1) Pole Δ AB^→=[−8,4] AC^→=[−9,−3]

	1		60
PΔ=		*|(−8)*(−3)−4*(−9)|=		=30
	2		2

2)

	a*b*c
Można skorzystać z wzoru na pole PΔ=
	4R

|AB|=√8²+4²=4√5 |AC|=√9²+3²=3√10 BC^→=[−1,−7] |BC|=√50=5√2

	4√5*3√10*5√2
30=
	4R

120R=60*10 R=5 ==== II sposób 1) POle − bez wyznacznika |AB|=4√5 |AC|=3√10 AB^→ o AC^→=(−8)*(−9)+4*(−3)=60 iloczyn skalarny 60=|AB|*|AC|*cosα 60=4√5*3√10*cosα

	1
cosα=		, to α=45o
	√2

	1		√2
PΔ=		*4√5*3√10*sin45o=6√50*		⇔
	2		2

P_Δ=30 2) Promień okręgu opisanego innym sposobem niż powyżej : a) symetralna AB ( jako zbiór wszystkich punktów jednakowo odległych od końców odcinka) A=(6,−1), B=(−2,3), C=(−3,−4). (x−6)²+(y+1)²=(x+2)²+(y−3)²⇔y=2x−3 symetralna AC: (x−6)²+(y+1)²=(x+3)²+(y+4)²⇔y=−3x+2 b) S− punkt przecięcia symetralnych− środek okręgu opisanego na Δ 2x−3=−3x+2 x=1, y=−1 S=(1,−1) R=|AS|=5 ==========

chichi: Ten I sposób to jest właśnie dokładnie to, co ja zrobiłem, drugi też jest okej, ale trzeba się nieco więcej napracować, taki bardziej dla podstawy, I dla rozszerzenia

Mila: Wykorzystując symetralne nie trzeba liczyć pola Δ i rachunków mało

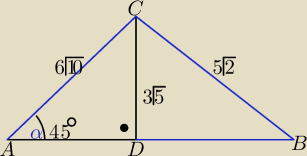
mat: Prosta AB : x+2y−4=0 |CD| − odległość C od AB

	|−3−8−4|
to |CD|=		= 3√5
	√5

	|CD|		√2
sinα =		=		to α=45o
	|AC|		2

	|BC|		5√2
R=		=		=5
	2sinα		√2

mat: Na rysunku ma być |AC|=3√10

chichi: Napisać równanie dwóch prostych, rozwiązać układ równań, policzyć odległość między punktami, to więcej pracy