Diagramy dla iloczynu kartezjanskiego anonim123: Jak za pomocą diagramów rozrysować zbiory z iloczynem kartezjańskim? Może ktoś sprawdzić czy dany przykład jest poprawny i ja na tej podstawie zrobię kolejne? Przykład do rozrysowania Ax(BuC)=(AxB)u(AxC)

chichi: Dla podanego przykładu równość zbiorów zachodzi, teraz bierz się za dowód

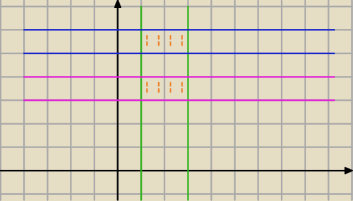
chichi: Iloczyn kartezjański odwołuje się do kartezjańskiego układu współrzędnych, zatem przedstawiamy go na płaszczyźnie, a nie za pomocą diagramów (choć tak też pewnie jakoś można, ale na pewno nie jest to lepszy sposób zobrazowania) Niech: A = [1, 3], B = [3, 4], C = [5, 6], B∪C = [3,4] ∪ [5, 6], A×(B∪C)

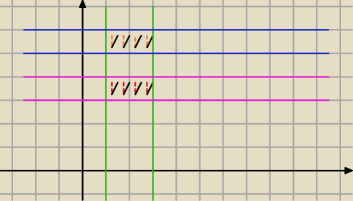
chichi: No i analogicznie: A = [1, 3] , B = [3, 4] , C = [5, 6] , wówczas: A×B, A×C, zatem A×B∪A×C = (A×B)∪(A×C)

anonim123: Ale nie wiem czy wykładowca nie zapyta mnie o diagramy bo mieliśmy ich użyć

chichi: Pyta o diagramy, a nawet nie pokazał o jakie diagramy mu chodzi? Może mój sposób zobrazowania iloczynu kartezjańskiego na płaszczyźnie nazywa diagramem?

chichi: A×(B∪C) = (A×B)∪(A×C) Niech 〈x,y〉 ∊ P będzie dowolne. 〈x,y〉 ∊ P ↔ 〈x,y〉 ∊ (A×B)∪(A×C) ↔ 〈x,y〉 ∊ A×B ∨ 〈x,y〉 ∊ A×C ↔ (x ∊ A ∧ y∊B) ∨ (x ∊ A ∧ y ∊ C) ↔ x ∊ A ∧ (y ∊ B ∨ y ∊ C) ↔ x ∊ A ∧ y ∊ B∪C ↔ 〈x,y〉 ∊ A×(B∪C) ↔ 〈x,y〉 ∊ P Z dowolności 〈x,y〉 otrzymujemy równość: A×(B∪C) = (A×B)∪(A×C) □

anonim123: Wydaje mi się że mieliśmy wykorzystać coś takiego https://zapodaj.net/5a3eaaedeba5b.jpg.html

chichi: Pierwsze widzę, aby ktoś używał diagramów Venne'a do przedstawienia graficznego produktu kartezjańskiego... Ale takie zobrazowanie za pomocą diagramu już jest jak najbardziej sensowne: https://zapodaj.net/becaae2ecb2aa.png.html

anonim123: Dobrze dzięki za pomoc 😄

chichi: Przez 〈x,y〉 oczywiście rozumiem parę uporządkowaną czyli zbiór { {x}, {x,y} }, gdzie element 'x' nazywamy pierwszą współrzędną, a element 'y' drugą współrzędną pary 〈x,y〉

chichi: Zostawiam przykład dla Ciebie do formalnego przeprowadzenia rozumowania, tak jak 13:53 A×(B\C) = (A×B) \ (A×C)

anonim123: Skąd się wzięła ta linijka? ↔ x ∊ A ∧ (y ∊ B ∨ y ∊ C)

anonim123: ? Z jakiego to jest prawa ?

chichi: Prawo rozdzielności koniunkcja względem alternatywy, z którego już korzystałem przy okazji dowodzenia równości innych zbiorów w zadaniu, które wrzucałaś poprzednio, ciekawi mnie dlaczego przy okazji tamtego zadania nie padło to pytanie?

anonim123: A w tym zadaniu coś robię źle? Nie wiem co dalej. https://zapodaj.net/8632236296303.jpg.html https://zapodaj.net/2b1e807e70918.jpg.html

anonim123: ?

chichi: Dlaczego nie odpowiadasz na moje pytania? A ja mam na Twoje odpowiadać Nie widzisz, że x∊A ∧ y∊B ∧ x∊A ∧ y∊C ↔ x∊A ∧ y∊B ∧ y∊C

anonim123: Dzięki nie odpowiadam bo chcę zrobić zadania na jutro i nie mam czasu na inne przykłady 😏

chichi: Nazywa się to prawem idempotentności koniunkcji, naprawdę wróć do teorii, a dopiero zadania

chichi: Miałem na myśli odpowiedź na pytanie z 15:09, zacznij studiować matematykę, a nie rozwiązywać na potęgę zadania..

anonim123: Ale wtedy nie wychodzi Ax(B iloczyn C)

chichi: Brak mi sił, no jak nie wychodzi... ? x∊A ∧ y∊B ∧ x∊A ∧ y∊C ↔ x∊A ∧ y∊B ∧ y∊C ↔ x∊A ∧ y∊B∩C ↔ 〈x,y〉∊A×(B∩C) ↔ 〈x,y〉∊L □

anonim123: Dzięki 😁