rozwiąż równanie
Emilia : |x−3|+|x+5|≥8
20 paź 16:55
Mila:
1) Z definicji i własności :
|a|≥0, |a|=|−a|
|a|+|b|≥|a+b|
2) |x−3|+|x+5|=|x−3|+|−x−5|≥|x−3−x−5|=|−8|=8
Czyli
|x−3|+|x+5|≥8 dla każdego x∊R , przy czym równość zachodzi dla x∊<−5,3>
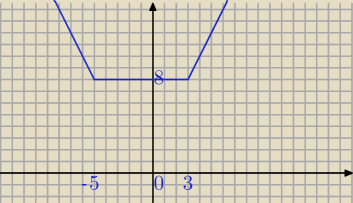
3) na rysunku masz wykres y=|x−3|+|x+5|
20 paź 17:16
Emilia : czyli jeżeli rozwiązuje to w ten sposób
1) (−∞; −5⟩
−x+3−x−5≥8
x≤−5
x∈(−∞ ;−5⟩
2) (−5; 3⟩
−x+3+x+5≥8
8≥8
x∈R
3)(3; +∞)
x−3+x+5≥8
x≥3
x∈(3;+∞)
I w jednym z przedziałów wychodzi R wtedy wszystkie x należą do R?
20 paź 17:24
Szkolniak: Jeśli w jednym z przypadków wychodzi, że x∊ℛ, to wtedy bierzesz cały przedział (dziedzinę) z
tego przypadku, tzn. w Twoim przykładzie bierzesz z drugiego wariantu przedział (−5;3>.
20 paź 17:35
Mila:
Trzeba dać między (1),(2),(3) spójnik "lub", co daje sumę przedziałów równą R.
W (2) powinna być odpowiedź : x∊(−5; 3⟩
20 paź 17:48
Emilia : okay dziękuje bardzo już rozumiem
20 paź 17:50
 1) Z definicji i własności :
|a|≥0, |a|=|−a|
|a|+|b|≥|a+b|
2) |x−3|+|x+5|=|x−3|+|−x−5|≥|x−3−x−5|=|−8|=8
Czyli
|x−3|+|x+5|≥8 dla każdego x∊R , przy czym równość zachodzi dla x∊<−5,3>
3) na rysunku masz wykres y=|x−3|+|x+5|
1) Z definicji i własności :
|a|≥0, |a|=|−a|
|a|+|b|≥|a+b|
2) |x−3|+|x+5|=|x−3|+|−x−5|≥|x−3−x−5|=|−8|=8
Czyli
|x−3|+|x+5|≥8 dla każdego x∊R , przy czym równość zachodzi dla x∊<−5,3>
3) na rysunku masz wykres y=|x−3|+|x+5|