Rozłóż wektor na składowe
Michał:
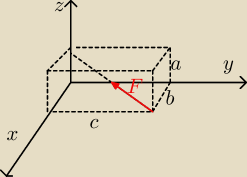
Znając a,b,c oraz wartość F, podaj składowe wektora F.
Wiem, że są wzory jakieś z cosinusem, a także takie z pierwiastkiem kwadratowym w mianowniku,
ale nie wiem jak do tego dojść.
19 paź 19:03
Michał: Pomocy

19 paź 20:37
Szkolniak: Nie wiem czy moja wiedza cokolwiek pomoże w tym problemie, ale może coś ruszę temat.
Zastanawiam się, czy jesteśmy w stanie jednoznacznie wyznaczyć ten wektor, tzn. punkt jego
początku i punkt jego końca? Jego składowe?
Początek wektora F zaczepiony jest w punkcie P=(b,c,0)
Niech koniec wektora F zaczepiony będzie w punkcie Q=(p,q,r)
Wtedy →
F = [p−b, q−c, r]
Nie do końca wiem czy rozumiem problem.. może ktoś jeszcze się wypowie

19 paź 21:02
Michał: Dobra, problem rozwiązany

Jeśli jesteś zainteresowany − Szkolniak, to mogę rozpisać, jeżeli
nie to zamykam

19 paź 21:48
Szkolniak: Rozpisz

chętnie zobaczę co i jak
19 paź 22:09
Michał:
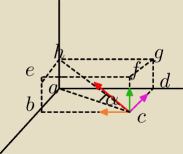
I sposób:
Zielona F
z, Różowa F
x, Pomarańczowa F
y (wektory)
W trójkącie ACH, sinα=a /
√a2+b2+c2 (przekątna prostopadłościanu) oraz AC=Fcosα
Zatem F
z=F*sinα=F*a /
√a2+b2+c2
W trójkącie ABC F
y=ACcosβ=Fcosαcosβ=F * |AC|/|CH| * |BC|/|AC| = F*|BC|/|CH| =
= F*c /
√a2+b2+c2
I analogicznie w dla F
x, tyle że będzie F*b /
√a2+b2+c2
Oraz przyjmujemy, że F
x i F
y są ujemne, bo są skierowane przeciwnie do osi kolejno x i y,
czyli ostatecznie współrzędne:
F=[ −F*b /
√a2+b2+c2, −F*c /
√a2+b2+c2, F*a /
√a2+b2+c2 ]
II sposób nieco intuicyjny lub strzelający:
Wiadomo, że wektory będą postaci F * α /
√a2+b2+c2, gdzie α to jest jakaś stała, w
tym przypadku bok klocka (z teorii o wektorach 3d lub z tego co jest wyżej wykazane, ale sami
nie wiemy jak to zrobić)
Wiemy, że wektor F
x działa na boku b, więc α
x=b, wektor F
y na c, więc α
y=c oraz α
z=a.
Wystarczy zatem tylko dobrać odpowiednie znaki dla odpowiednich składowych, i wychodzi nam to
samo, tylko bez przekształceń.
19 paź 22:56
Michał: "czyli ostatecznie współrzędne:" → ostatecznie składowe*
19 paź 22:57
Szkolniak: Dzięki
Michał 
22 paź 19:54
 Znając a,b,c oraz wartość F, podaj składowe wektora F.
Wiem, że są wzory jakieś z cosinusem, a także takie z pierwiastkiem kwadratowym w mianowniku,
ale nie wiem jak do tego dojść.
Znając a,b,c oraz wartość F, podaj składowe wektora F.
Wiem, że są wzory jakieś z cosinusem, a także takie z pierwiastkiem kwadratowym w mianowniku,
ale nie wiem jak do tego dojść.


 Jeśli jesteś zainteresowany − Szkolniak, to mogę rozpisać, jeżeli
nie to zamykam
Jeśli jesteś zainteresowany − Szkolniak, to mogę rozpisać, jeżeli
nie to zamykam 
 chętnie zobaczę co i jak
chętnie zobaczę co i jak
 I sposób:
Zielona Fz, Różowa Fx, Pomarańczowa Fy (wektory)
W trójkącie ACH, sinα=a / √a2+b2+c2 (przekątna prostopadłościanu) oraz AC=Fcosα
Zatem Fz=F*sinα=F*a / √a2+b2+c2
W trójkącie ABC Fy=ACcosβ=Fcosαcosβ=F * |AC|/|CH| * |BC|/|AC| = F*|BC|/|CH| =
= F*c / √a2+b2+c2
I analogicznie w dla Fx, tyle że będzie F*b / √a2+b2+c2
Oraz przyjmujemy, że Fx i Fy są ujemne, bo są skierowane przeciwnie do osi kolejno x i y,
czyli ostatecznie współrzędne:
F=[ −F*b / √a2+b2+c2, −F*c / √a2+b2+c2, F*a / √a2+b2+c2 ]
II sposób nieco intuicyjny lub strzelający:
Wiadomo, że wektory będą postaci F * α / √a2+b2+c2, gdzie α to jest jakaś stała, w
tym przypadku bok klocka (z teorii o wektorach 3d lub z tego co jest wyżej wykazane, ale sami
nie wiemy jak to zrobić)
Wiemy, że wektor Fx działa na boku b, więc αx=b, wektor Fy na c, więc αy=c oraz αz=a.
Wystarczy zatem tylko dobrać odpowiednie znaki dla odpowiednich składowych, i wychodzi nam to
samo, tylko bez przekształceń.
I sposób:
Zielona Fz, Różowa Fx, Pomarańczowa Fy (wektory)
W trójkącie ACH, sinα=a / √a2+b2+c2 (przekątna prostopadłościanu) oraz AC=Fcosα
Zatem Fz=F*sinα=F*a / √a2+b2+c2
W trójkącie ABC Fy=ACcosβ=Fcosαcosβ=F * |AC|/|CH| * |BC|/|AC| = F*|BC|/|CH| =
= F*c / √a2+b2+c2
I analogicznie w dla Fx, tyle że będzie F*b / √a2+b2+c2
Oraz przyjmujemy, że Fx i Fy są ujemne, bo są skierowane przeciwnie do osi kolejno x i y,
czyli ostatecznie współrzędne:
F=[ −F*b / √a2+b2+c2, −F*c / √a2+b2+c2, F*a / √a2+b2+c2 ]
II sposób nieco intuicyjny lub strzelający:
Wiadomo, że wektory będą postaci F * α / √a2+b2+c2, gdzie α to jest jakaś stała, w
tym przypadku bok klocka (z teorii o wektorach 3d lub z tego co jest wyżej wykazane, ale sami
nie wiemy jak to zrobić)
Wiemy, że wektor Fx działa na boku b, więc αx=b, wektor Fy na c, więc αy=c oraz αz=a.
Wystarczy zatem tylko dobrać odpowiednie znaki dla odpowiednich składowych, i wychodzi nam to
samo, tylko bez przekształceń.
