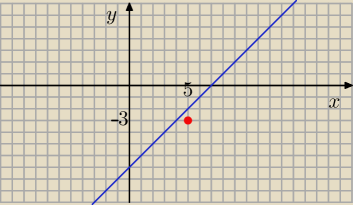
proszę o rozwiązanie anna: Okrąg wpisany w trójkąt ABC jest opisany równaniem x² + y² − 10x + 6y + 29 = 0. Punkty styczności tego okręgu z bokami AC i BC trójkąta ABC leżą na prostej o równaniu: x − y − 7 = 0 . Wyznacz współrzędne wierzchołka C trójkąta ABC . (x + 5)² + (x − 3)² =5 S = ( − 5 ; 3) r = √5 nie wiem co dalej

anna: żle zapisałam środek okręgu (x−5)² + (y + 3)² = 5 S =( 5 : −3) r =√5

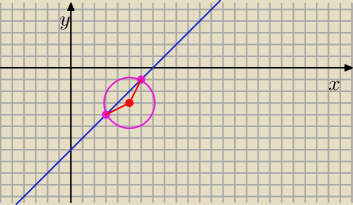
janek191: ( x − 5)² + ( y + 3)² = 5 S = ( 5, − 3) r =√5 ( x − 5)² + ( y + 3)² = 5 y = x − 7 Rozwiąż ten układ równań.

janek191:

janek191: Dokończ

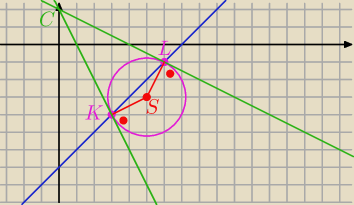
janek191: K = ( 3, − 4) L = ( 6, − 1) Proste: y = − 2 x + 2 i y = −¹ ₂ c + 2

janek191: Miało być y = −¹₂ x + 2

anna: obliczyłam że C = (0 ; 2) czy to jest dobrze dziękuję bardzo

janek191:

janek191: A jak wyznaczyłaś równania prostych?

chichi: Nie trzeba wyznaczać równań dwóch prostych

anna: układ równań dla prostych KC i LC ponieważ KC ⊥ SK i LC ⊥ SL

janek191:

Mila: II sposób: 1) Równanie stycznej do okręgu w P=(x₀,y₀)∊okręgu o środku S=(a,b) (x−a)²+(y−b)²=r² s: (x₀−a)*(x−a)+(y₀−b)*(y−b)=0 2) W twoim zadaniu: ( x − 5)² + ( y + 3)² = 5 K=(3,−4) styczna w K=(3,−4) : (3−5)*(x−5)+(−4+3)*(y+3)=0 dokończ

anna: styczna do okręgu w punkcie K = (3 ; −4) to y = −2x +7 styczna do okręgu w punkcie L = ( 6 ; −1) to

	−1		1
y =		x −
	2		2

czyli

	−1		1
−2x +7 =		x −		⇒ x = 5 to y = −3
	2		2

czyli C = (5 −3) ale ten wynik nie jest równy C = ( 0 ; 2) według mnie wynik powinien być taki sam gdzie jest błąd

chichi: Styczna do okręgu w punkcie K dana jest równaniem y = − 2x + 2

	1
Styczna do okręgu w punkcie L dana jest równaniem y = −		x + 2
	2

Widać po wyrazie wolnym, że przetną się w punkcie (0, 2). Nie wiem jak wyznaczalas równania tych stycznych, możesz pokazać?

janek191: K = (3, −4) S = ( 5, −3) Współczynnik kierunkowy prostej KS

	−3 − (−4)		1
a1 =		=
	5 − 3		2

więc współczynnik kierunkowy prostej KC do niej prostopadłej

	1
b1 = − 2 bo		*(−2) = − 1
	2

zatem y = b₁ x + k y = −2 x + k Podstawiam współrzędne K − 4 = −2*3 + k ⇒ k = 2 y = − 2 x + 2 ============= Dalej analogicznie L = ( 6, −1) S = ( 5 , − 3) itd.

anna: dziękuję bardzo ja sprawdzałam wzór na równanie stycznej którą podała Mila 19 paż 19:24 już rozwiązałam i C =(0 ;2)

Mila: 19:24 Wzór jest błędny. Literówka. Poprawka: Równanie stycznej do okręgu w P=(x₀,y₀)∊okręgu o środku S=(a,b) (x−a)²+(y−b)²=r² s: (x₀−a)*(x−x₀)+(y₀−b)*(y−y₀)=0 1) K = (3, −4)=(x₀,y₀), S = ( 5 , − 3) s₁: (3−5)*(x−3)+(−4+3) (y+4)=0⇔ −2*(x−3)−(y+4)=0 −2x+6−y−4=0 y=−2x+2 2) L = ( 6, −1) S = ( 5 , − 3) s₂: (6−5)(x−6)+(−1+3)*(y+1)=0⇔ x−6+2*(y+1)=0 x−6+2y+2=0 x+2y−4=0 x−4=−2y

	−1
y=		x+2
	2

====== 3)

−1
	x+2=−2x+2
2

x=0, y=2 C=(0,2) ============

anna: dziękuję jeszcze raz literówki zdarzają się