matematykaszkolna.pl
Wyznacz okres podstawowy funkcji sinus:
 π 
Wyznacz okres podstawowy funkcji f(x)=sin(x+
)
 2 
 π π 
f(x+T)=sin(x+T+
) tutaj chciałem podstawić T+
=2π ale odpowiedź to 2π, ktoś wie
 2 2 
dlaczego tak?
18 paź 23:44
wredulus_pospolitus: bo powinno być: sin(x +π/2) = sin(x + T + π/2) bo tak wygląda Twoja funkcja f(x)
19 paź 00:00
chichi: No jak?
 π π 
( f(x) = sin(x+
) ⇒ f(x+T0) = sin(x+
+T0) ) ⇒ T0 = 2π
 2 2 
19 paź 00:02
sinus: Czyli w tym przypadku tylko T biorę pod uwagę?
19 paź 00:06
chichi: Zerknij po prostu do definicji... https://pl.wikipedia.org/wiki/Funkcja_okresowa Bez korzystania z definicji:
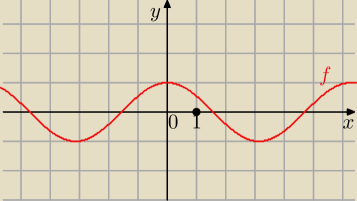
 π 
Wykres funkcji sin(x+
) powstał poprzez przesunięcie wykresu funkcji sin(x) o wektor
 2 
 π 
[−
, 0], zatem okres nie ulega zmianie w wyniku takiego przesunięcia
 2 
19 paź 00:16
sinus: Ok, dziękujęemotka
19 paź 00:25
mat:
 π 
sin(x+
)= cosx to T=2π
 2 
19 paź 00:34
janek191: rysunek
19 paź 09:11