Sprawdzenie rozwiązania zadania. niunie2k: Rzucamy dwa razy symetryczną sześcienną kostką do gry. Wypisz wszystkie możliwe wyniki rzutów w tabelce. Ile jest wyników, w których suma wyrzuconych oczek należy do zbioru rozwiązań nierówności x² − 8x + 12 < 0. Uzupełniłem tabele, delta równa się 16, x1 = 2, x2 = 6 Czy odpowiedź to że jest 6 wyników? Zaznaczyłem wszystkie 6 w tabeli oraz jedną 2.

I'm back: A co z tymi wyrzucanymi wynikami robisz?

niunie2k: wszystkie możliwe wyniki wpisałem do tabeli

I'm back: Masz mozliwosci 1,3 − 3,1 1,4 − 4,1 2,2 2,3 − 3,2 Czyli w sumie 7 możliwości

niunie2k: suma 1,3 to 4, x1 wynosi 2 a x2 wynosi 6, dlaczego mam to wpisac jako mozliwosc? Jakbys mogl to wytlumacz bo nie rozumiem za bardzo haha

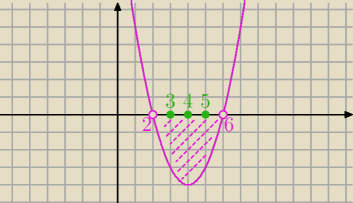
chichi: x²−8x+12 < 0 ⇔ x∊(2, 6) Zatem interesują nas sumy oczek ze zbioru {3, 4, 5} (1) A − suma oczek równa 3, A = {(1, 2), (2, 1)} ⇒ |A| = 2 (2) B − suma oczek równa 4, B = {(1, 3), (3, 1), (2, 2)} ⇒ |B| = 3 (3) C − suma oczek równa 5, C = {(1,4), (4, 1), (2, 3), (3, 2)} ⇒ |C| = 4 |A| + |B| + |C| = 2 + 3 + 4 = 9

niunie2k: dlaczego suma oczek rowna 3,4,5 jak x1 i x2 to 2 i 6? Nie za bardzo rozumiem

chichi: Rozwiąż proszę tę nierówność x² − 8x + 12 < 0 i podaj zbiór rozwiązań nierówności

chichi:

niunie2k: dobra, całkowicie mi się pomyliło, teraz rozumie hahahah

niunie2k: dziękuje bardzo jeszcze raz za pomoc

chichi: @wredulus₋pospolitus zapomniałeś o sumie oczek równej 3

chichi: @niunie2k na zdrowie