Pomoc z zadaniem. Maciek: Rzucamy dwa razy symetryczną sześcienną kostką do gry. Wypisz wszystkie możliwe wyniki rzutów. Ile jest wyników, w których iloczyn wyrzuconych oczek należy do zbioru rozwiązań nierówności x² − 6x + 16 ≤ 0 Rozpisałem wszystkie możliwe wyniki rzutów, lecz co dalej? Próbując obliczyć deltę wychodzą mi jakieś niesamowite wyniki, nie jestem pewien czy jestem zaspany czy to zadanie jest bez sensu.

Maciek: Zatrzymuje się na momencie kiedy z delty wychodzi mi −28, już dalej nie wiem co mam totalnie zrobić.

chichi: x²−6x+16 = x²−6x+9+7 = (x−3)²+7 ≥ 7

Maciek: O kurcze, mógłbym mi wytłumaczyć co dokładnie zrobiłeś?

chichi: Niech f(x) = x²−6x+16 wówczas ja pokazałem, że f_min(x) = 7, a oni się pytają kiedy funkcja f przyjmuje wartości mniejsze bądź równe zero.. Odpowiedź brzmi nigdy! Nie ma takiego 'x'

chichi: Zatem zbiór rozwiązań tej nierówności jest zbiorem pustym, zatem odp. do zadania to?

Maciek: Jest 0 wyników?

chichi: Voilà

Maciek: Coś sądzę że jak tak zapisze to nauczycielka się trochę przypie*doli, ale jakoś dam radę, przecież w końcu wykonałem zadanie haha

chichi: To możesz zrobić również tak: Niech f(x) = x²−6x+16 (1) a > 0

	b		−6
(2) p = −		= −		= 3
	2a		2*1

(3) Δ = b²−4ac = (−6)²−4*1*16 = −28 < 0 (brak miejsc zerowych)

	Δ		28
(4) q = −		= −		= 7
	4a		4*1

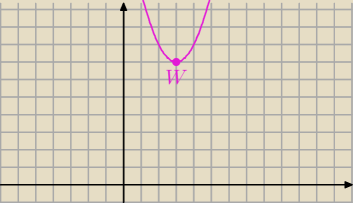
(5) W = (3, 7) Z powyższych obserwacji możemy stwierdzić iż zbiorem wartości funkcji f jest zbiór [7, +∞], zatem funkcja f nie przyjmuje wartości niedodatnich, stąd zbiorem rozwiązań nierówności x²−6x+16 ≤ 0 jest zbiór pusty, to już powinna uznać (tamto oczywiście też)

mat: Δ<0 i ramiona paraboli do góry to f(x)≤0 − sprzeczność x∊∅ p=0

chichi: Rzecz jasna zbiorem wartości funkcji jest zbiór [7, +∞) byłem skupiony na pisaniu tekstu i przypadkiem dałem nawias domknięty przy nieskończoności... dureń ze mnie