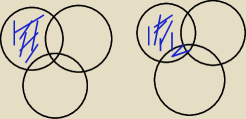18 paź 20:12
anonim123: zaraz obrócę
18 paź 20:12
18 paź 20:14
student: lepiej więcej kroków zrobić
18 paź 20:21
Sushi:
Zawsze można zrobić pomocniczy rysunek
aby coś zauważyć czy to dla obliczeń czy dla dowodu/kontrprzykladu
18 paź 20:23
anonim123: ale to jest dobrze?
18 paź 20:24
Sushi:
Włączają się głupie pozwolenia na wyświetlenia reklam
Możesz tutaj zrobić rysunek
18 paź 20:28
chichi:
Diagramy Venne'a są zrobione poprawne, ale w logice te diagramy możesz sobie jedynie zachować
dla siebie. W tym przypadku nierówność zbiorów należy pokazać formalnie, korzystając z praw
rachunku zbiorów

18 paź 20:29
anonim123:
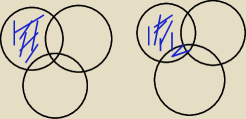
18 paź 20:35
chichi:
Może powinienem to napisać tak: w tym przypadku, aby pokazać, że nie zachodzi równość zbiorów,
należy zrobić to formalnie, korzystając z praw rachunku zbiorów, bo 'nierówność zbiorów' brzmi
przynajmniej myląco.. Polska język, trudna język...

18 paź 20:42
anonim123: wiem, ale wykładowca pozwolił nam korzystać z diagramów w tym ćwiczeniu i jeżeli wyjdzie
równość
to mamy dowodzić ale jeżeli nie to podać kontrprzykład

18 paź 20:44
student: lepiej 8 przypadków zrobić
18 paź 20:44
anonim123: to dobrze jest to narysowane?
18 paź 20:50
chichi:
Proszę przeczytaj moją wypowiedź z
20:29, bo odnoszę wrażenie, że na marne pisałem

18 paź 20:52
anonim123: dzięki

18 paź 20:55
anonim123: A może ktoś podać jakiś kontrprzykład do (AuC)\C=A?

19 paź 15:38
chichi:
A = {1, 2, 3, 4, 5} ∧ C = {3, 4, 5, 6, 7}
A∪C = {1, 2, 3, 4, 5, 6, 7}
(A∪C) \ C = {1, 2} ⇒ [(A∪C) \ C] ⊂ A
19 paź 15:43
19 paź 16:05
chichi:
Widzę, że przykład wyżej został rozwiązany 'formalnie' zrób tak również i tutaj, tak diagram
Venne'a jest dobrze narysowany ten ostatnia z prawa

19 paź 16:16
chichi:
Ale jeżeli rozumiem te Twoje zapisy, to z lewa jest diagram symbolizujący zbiór znajdujący się
po lewej stronie równania i nie jest on poprawnie narysowany..

19 paź 16:17
chichi:
Albo zaznacz po prostu gdzie jest odpowiedź końcowa na tych diagramach, a nie maziasz se
kolorkami i Bóg wie co Ty uznajesz za odpowiedź

19 paź 16:18
19 paź 16:23
chichi:
No i super, już wiesz z diagramów Venne'a, że owa równość zbiorów zachodzi. No to zacznijmy
dowodzić to formalnie, proponuję tak: przypuśćmy, że dowolny 'x' należy do zbioru znajdującego
się z prawej strony równania, korzystając z praw rachunku zbiorów pokażemy, że należy wówczas
do zbioru znajdującego się z lewej strony i wówczas równość owych zbiorów stwierdzimy na mocy
aksjomatu ekstensjonalności (lepiej zawsze wyjść od bardziej rozbudowanego zbioru)

19 paź 16:27
chichi:
Spróbuj zacząć, a ja w razie w pomogę

19 paź 16:27
19 paź 16:30
chichi:
Ooo ja nawet nie widziałem tego linku, musiałem go przeoczyć, @
ite pewnie, przecież to
bzdura co jest tam napisane

19 paź 16:34
anonim123: To jak to zrobić?

19 paź 16:43
chichi:
A \ (B \ C) = (A \ B) ∪ (A ∩ C)
Niech x ∊ P będzie dowolny, wówczas:
x ∊ P ↔ x ∊ (A \ B) ∪ (A ∩ C) ↔ x ∊ A \ B ∨ x ∊ A ∩ C ↔
↔ (x ∊ A ∧ ¬x ∊ B) ∨ (x ∊ A ∧ x ∊ C) ↔ x ∊ A ∧ (¬x ∊ B ∨ x ∊ C) ↔
↔ x∊ A ∧ ¬(x ∊ B ∧ ¬x ∊ C) ↔ x ∊ A ∧ ¬x ∊ B \ C ↔ x ∊ A \ (B \ C) ↔ x ∊ L
Zatem z dowolności x otrzymujemy równość A \ (B \ C) = (A \ B) ∪ (A ∩ C) □

19 paź 16:55
anonim123: Dzięki

19 paź 20:45