Czy funkcja jest okresowa sinus: Czy funkcja f(x)=sin²x jest okresowa? f(x+T) = sin²(x+T)=(sin(x+T))² = (sin(x+2π))² = (sinx)² = sin²x = f(x) czyli to f. okresowa Moje pytanie to czemu za T podstawiamy 2π i czemu potem ono znika? 2. f(x) = sinx² f(x+T) = sin(x+T)² = sin(x²+2xT+T²) f. nie jest okresowa, bo przy T stoi x Moje pytanie co zrobić gdyby nie było tego x przy T i czemu ten x przeszkadza?

wredulus_pospolitus: podstawiamy 2π bo wiemy że okresem funkcji g(x) = sinx jest właśnie 2π ... a znika ... bo to jest okres funkcji g(x) = sinx albo jak wolisz − stosujemy wzory redukcyjne

wredulus_pospolitus: Tx powoduje że nie masz stałego okresu ... ponieważ chcemy uzyskać: sin(x²) = sin(x² + 'coś' ) a to 'coś' musi być postaci 2k*π (najlepiej 2π) bo taki okres ma funkcja sin x. tym 'coś' u Ciebie jest Tx + T² ... gdyby nie było tego 'x' to byśmy mieli T + T² = 2π −−> T² + T − 2π = 0 −−−> możemy wyznaczyć T₁ i T₂ dla których będziemy mieli rozwiązanie. natomiast ten 'x' wszystko psuje, ponieważ: Tx + T² = 2π −−−> T² + Tx − 2π = 0 będzie miało jakieś T₁ i T₂ dla x=1 ... ale INNE wartości T₁ i T₂ dla wartości x=2, a jeszcze inne dla wartości x = 2√2π, itd. związku z tym −> 'okres' zależy od wartości zmiennej x, co przeczy temu że jest stały (i niezależny od zmiennej x).

sinus: Ok, rozumiem, a co jeśli miałbym na przykład (sin(x+4π))² ? Co wtedy dzieje się z tym 4π?

wredulus_pospolitus: wzory redukcyjne: sin(x+4π) = sin(x + 2*2π) = sinx

sinus: Okej, dziękuję

sinus: Jednak mam jeszcze jedno pytanie co gdyby było (sin(x+2T))² wtedy 2T=2π −> T=π ? czy aby udowodnić że dana funkcja jest okresowa trzeba f(x+T) sprowadzić do f(x)?

wredulus_pospolitus: zauważ, że T oznacza najmniejszy możliwy okres ... aby wykazać okresowość funkcji wystarczy wykazać, że istnieje 't' (dowolny okres).

sinus: Jasne, dzięki wielkie

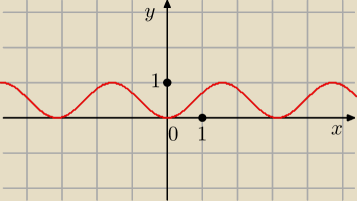
janek191: f(x) = sin² x

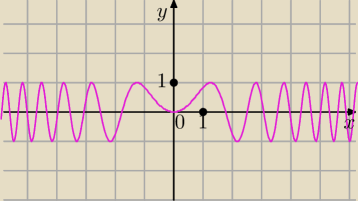
janek191: f(x0 = sin(x²)

janek191: f(x) = sin (x²)