proszę o rozwiązanie anna: Punkt S jest punktem przecięcia się środkowych trójkąta równoramiennego ABC o podstawie AB . Okrąg o średnicy AB ma równanie x2 + y2 + 12x− 10y + 44 = 0 , a cięciwa tego okręgu równoległa do prostej AB i przechodząca przez punkt S zawiera się w prostej o równaniu x − y + 14 = 0 . Wyznacz równanie okręgu o środku C , który przechodzi przez punkty A i B .

chichi:

	21		19		115
O: (x+		)2 + (y−		)2 =
	2		2		2

Co zrobiłaś na razie @anna ? P.S. Zgadza się wynik?

anna: nie mam wyniku tego zadania nie wiem jak doszedł do takiego wzoru prosiłabym o rysunek do treści zadania

Mariusz: x²+y²+12x−10y+44=0 x²+12x+36 + y²−10y+25=17 (x+6)²+(y−5)²=17 Po przepisaniu równania okręgu otrzymaliśmy środek okręgu O = (−6,5) oraz promień okręgu r = √17 AB to średnica okręgu zatem |AB| = 2√17 Z tego że AB to średnica okręgu o równaniu (x+6)²+(y−5)²=17 mamy także że x_A+x_B = −12 y_A+y_B = 10 Z tego że prosta przechodząca przez punkty A oraz B jest równoległa do prostej o równaniu x−y+14=0 mamy że y_B−y_A=x_B−x_A (Współczynnik kierunkowy prostej to iloraz przyrostu wartości rzędnych do przyrostu wartości odciętych a że punkty A oraz B są różne to przyrost odciętych jest niezerowy i po pomnożeniu współczynnika kierunkowego przez przyrost odciętych otrzymujesz powyższą równość) |AB| = 2r |AB| = 2√17 √(x_B−x_A)²+(y_B−y_A)²=2√17 (x_B−x_A)²+(y_B−y_A)²=68 2(x_B−x_A)²=68 (x_B−x_A)²=34 |x_B−x_A| = √34 I teraz mamy dwie możliwości x_B−x_A = √34 albo x_B−x_A = −√34 Dla pierwszej możliwości mamy układy równań x_A+x_B = −12 x_A−x_B = −√34 oraz y_A+y_B = 10 y_A−y_B = −√34

	−12−√34		10−√34
xA =		yA=
	2		2

	−12+√34		10+√34
xB =		yB=
	2		2

Czyli pierwsza możliwa para punktów A,B ma współrzędne

	−12−√34		10−√34
A = (		,		)
	2		2

	−12+√34		10+√34
B = (		,		)
	2		2

Sprawdźmy czy dla tej drugiej możliwości punkty A oraz B zamienią się miejscami x_A+x_B = −12 x_A−x_B = √34 oraz y_A+y_B = 10 y_A−y_B = √34

	−12+√34		10+√34
xA =		yA=
	2		2

	−12−√34		10−√34
xB =		yB=
	2		2

Tak jak podejrzewałem dla drugiej możliwości punkty A oraz B zamieniły się miejscami Skoro trójkąt jest równoramienny to √(x_C−x_A)²+(y_C−y_A)²=√(x_C−x_B)²+(y_C−y_B) Punkt S leży na prostej o równaniu x−y+14=0 więc y_S=x_S+14 Punkt S dzieli odcinek OC gdzie O to środek okręgu (x+6)²+(y−5)²=17

Mariusz: w stosunku 2:3

|SC|		2
	=
|OC|		3

3|SC| = 2|OC| 3√(x_C − x_S)²+(y_C − x_S − 14)²=2√(x_C+6)²+(y_C − 5)² (x_C−x_A)²+(y_C−y_A)² = (x_C−x_B)²+(y_C−y_B)² 9(x_C − x_S)²+9(y_C − x_S − 14)²=4(x_C+6)²+4(y_C − 5)² Teraz mamy dwa równania i trzy niewiadome x_C , y_C oraz x_S Jeżeli uda ci się znaleźć współrzędne punktu S to z powyższego układu równań znajdziemy współrzędne punktu C Na razie nie mam pomysłu na obliczenie współrzędnych punktu S Gdy obliczysz współrzędne wierzchołków tego trójkąta równoramiennego ABC łatwo napiszesz równanie okręgu

chichi: @Mariusz rozwiązanie nieco długie, później pokaże nieco inne. Ale podpowiem jak dobrać się do współrzędnych punktu S, AB jest podstawą trójkąta równoramiennego zatem prosta zawierająca wysokość jest zarazem prosta zawierająca środkową poprowadzoną z wierzchołka C, jest ona prostopadła do AB, ba jest również prostopadła do x−y+14=0, znajdź środek AB i wyznacz tą prostą, a następnie rozwiąż układ równań składający się z równania otrzymanej prostej oraz x−y+14=0, tak otrzymasz współrzędne punktu S

Mariusz: chichi właśnie brakowało mi tego jednego równania aby wyznaczyć współrzędne punktu S Po obliczeniu współrzędnych punktu S i wstawieniu do układu równań z wpisu z 14 paź 2021 13:04 otrzymałem dwa możliwe współrzędne punktu C Czyżbyśmy mieli dwa takie okręgi a może jedno rozwiązanie układu równań z wpisu z 14 paź 2021 13:04 należy odrzucić

chichi:

	xA+xB+xC
Jest tylko jeden punkt C, sprawdź ze wzoru czy		= xS oraz dla drugiej
	3

współrzędnej. Jakie współrzędne dla punktów C otrzymałeś?

Mariusz: y=−x+b 5=6+b b = −1 y=−x−1 y=x+14 x+14=−x−1 2x=−15

	15
x=−
	2

	15		28
y = −		+
	2		2

	13
y =
	2

	15		13
S = (−		,		)
	2		2

Wstawiając współrzędne punktu S do układu równań z wpisu z 14 paź 2021 13:04 otrzymujemy (x_C−x_A)²+(y_C−y_A)²=(x_C − x_B)²+(y_C − y_B)²

	15		13
9(xC+		)2+(yC −		)2 = 4(xC+6)2+4(yC−5)2
	2		2

	(−12+√34)2		(10+√34)2
xC2−(−12+√34)xC+		+yC2 −(10+√34)yC+		=
	4		4

	(−12−√34)2		(10−√34)2
xC2−(−12−√34)xC+		+yC2−(10−√34)yC+
	4		4

	225		169
9(xC2+15xC+		)+9(yC2−13yC+		)=
	4		4

4(x_C²+12x_C+36)+4(y_C²−10y_C+25) −2√34x_C−2√34y_C

	(−12+√34+12+√34)(−12+√34−12−√34)
+		+
	4

(10+√34−10+√34)(10+√34+10−√34)
	=0
4

	2025		1521
9xC2+135xC+		+9yC2−117yC+		=
	4		4

4x_C²+48x_C+144+4y_C²−40y_C+100 −2√34x_C−2√34y_C−12√34+10√34=0

	1285
5xC2+87xC+5yC2−77yC+		=0
	2

−2√34x_C−2√34y_C−2√34=0

	1285
5xC2+87xC+5yC2−77yC+		=0
	2

x_C+y_C+1=0

	1285
5xC2+87xC+5yC2−77yC+		=0
	2

y_C=−x_C−1

	1285
5xC2+87xC+5(−xC−1)2−77(−xC−1)+		=0
	2

y_C=−x_C−1

	1285
5xC2+87xC+5xC2+10xC+5+77xC+77+		=0
	2

y_C=−x_C−1

	164+1285
10xC2+174xC+		=0
	2

y_C=−x_C−1

	1449
10xC2+174xC+		=0
	2

y_C=−x_C−1 100x_C²+1740x_C+7245 = 0 y_C=−x_C−1 (10x_C+87)²+7245−7569=0 y_C=−x_C−1 (10x_C+87)²−324=0 y_C=−x_C−1 (10x_C+87−18)(10x_C+87+18)=0 y_C=−x_C−1 (10x_C+69)(10x_C+105)=0

	69		59
C1 = (−		,		)
	10		10

	21		19
C2 = (−		,		)
	2		2

Widzisz z układu równań wychodzą dwa punkty C z czego ten drugi pokrywa się z twoim

Mariusz: No fajnie czyli jedno rozwiązanie tego układu trzeba odrzucić a we wpisie z 14 paź 2021 14:40 podałeś warunek jaki musi być spełniony aby rozwiązanie zostawić

chichi: O=(−6, 5) ∧ |AB| = 2√17 {(x+6)²+(y−5) = 17 {x−y+14 = 0 {x = −10 {x = −5 {y = 4 ∨ {y = 9

	15		13
Niech: D=(−10, 4) ∧ E=(−5, 9) ⇒ S=(−		,		)
	2		2

y_AB: a = −1 ∧ O∊y_AB ⇒ y_AB = −x−1 2vec(OS) = vec(SC) zatem mamy, że:

	3		3		15		15		21		21		19
2[−		,		] = [c+		, −c−		] ⇒ c = −		⇒ C=(−		,		)
	2		2		2		2		2		2		2

	3√2		9√2
( |OS| =		⇒ |SC| = 3√2 ) ⇒ |OC| =
	2		2

	9√2		115
Z tw. Pitagorasa mamy, że: (√17)2+(		)2 = |AC|2 ⇒ |AC|2 =		= R
	2		2

	21		19		115
O: (x+		)2 + (y−		)2 =
	2		2		2

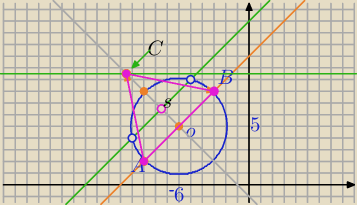
Mila: Punkt S jest punktem przecięcia się środkowych trójkąta równoramiennego ABC o podstawie AB . Okrąg o średnicy AB ma równanie x² + y² + 12x− 10y + 44 = 0 , a cięciwa tego okręgu równoległa do prostej AB i przechodząca przez punkt S zawiera się w prostej o równaniu x − y + 14 = 0 . Wyznacz równanie okręgu o środku C , który przechodzi przez punkty A i B . 1) Dany okrąg (x+6)²+(y−5)²=17 prosta y=x+14 2) Prosta AB: y=x+b, i o=(−6,5) ∊prostej AB y=x+11 3) Prostopadła do AB i przechodząca przez punkt O=(−6,5) k: y=−x−1 Jedna środkowa zawiera się w prostej k i C∊k S: −x−1=x+14

	−15		13
x=		, y=
	2		2

	−15		13
S=(		,		)
	2		2

4) Wsp. punktów A i B (x+6)²+(y−5)²=17 i y=x+11

	√34		√34		√34		√34
A=(−6−		, 5−		) i B=(−6+		, 5+		)
	2		2		2		2

5) Wsp. punktu C:

	15		√34   √34   −6− +(−6)+ +xc   2   2
−		=
	2		3

	21
−45/2=−12+xc⇔xc=−
	2

13		√34   √34   5− +5+ +yc   2   2
	=
2		3

39
	=10+yc
2

	19
yc=
	2

	21		19
C=(−		,		)
	2		2

6)

	115
rc2=|AC|2=
	2

dokończ

;): ....... początek jak u Mili

	15		13
S( −		,		) −− jest środkiem ciężkości trójkąta ABC
	2		2

→ → to OC=3OS ⇒ [x+6, y−5]=3[−3/2; 3/2]

	9		9		21		19		21		19
x+6=−		i y−5=		⇒ x=−		i y=		⇒C=(−		,		)
	2		2		2		2		2		2

	81
|OC|2=9|OS|2 =
	2

|AC|²=|BC|²=R ² to R²= |OC|²+r² , r²=17

	81		115
R2=		+17 =
	2		2

	21		19		115
o(C,R) : (x+		)2+(y−		)2=
	2		2		2

anna:

	SC		2
jak obliczyłeś stosunek		=		skąd to wiesz (Mariusz 13;04)
	OC		3

chichi: @anna rzuć okiem: https://www.geogebra.org/m/mFQPWNjt#:~:text=TWIERDZENIE%3A%20%C5%9Arodkowe%20w%20tr%C3%B3jk%C4%85cie%20przecinaj%C4%85,punktem%20przeci%C4%99cia%20%C5%9Brodkowych%20tr%C3%B3jk%C4%85ta%20ABC.

Mil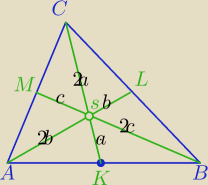a: anna środkowe Δ przecinają się w jednym punkcie , który dzieli je w stosunku 2:1 licząc od wierzchołka . K,L,M−środki boków Δ Dlatego wygodnie jest skorzystać z wektorów , jest mniej obliczeń .

anna: dziękuję bardzo wszystkim którzy byli zainteresowani tym zadaniem i pomogli mi zrozumieć szczególnie skorzystanie ze wzoru na współrzędną punktu C

xA +xB +xC
	= xs którego nie znałam
3

chichi: Na zdrowie