Proszę o pomoc
Kasia: Potrzebna pomoc
W czworokącie wpisanym w okrag dane są:
IABI=3, IADI=9, kąt BAF=120
oraz dwa pozostale boki mają długość 13√3
Oblicz pole tego czworokąta.
11 paź 23:42
chichi:
Jaki czworokąt, ABCD? Czym jest punkt F?
11 paź 23:46
Kasia: ABCD
11 paź 23:47
Kasia: Tam jest kąt BAD=1200
11 paź 23:48
chichi:
A druga część pytania?
11 paź 23:48
chichi:
Napisz proszę treść, a nie własnymi słowami
11 paź 23:50
Kasia: Niestety tak są sformuowane pytania na karcie.
Napisałam słowo w słowo 🤷♀️
11 paź 23:57
chichi:
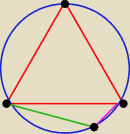
Zatem jeśli dobrze rozumiem polecenie, że pozostałe boki mają po 13
√3, to sytuacja jak na
rysunku, którego niestety nie mogę opisać z telefonu. Czerwony trójkąt jest równoboczny, a
jego bok jest długości
13√3, zielony odcinek jest długości
9, a różowy
3.
Szukane pole składa się z pola dwóch trójkątów, tego równobocznego oraz tego 'kolorowego' jego
| | 1 | |
pole to S = |
| *9*3*sin(120o), teraz wyznacz pole trójkąta równobocznego i dodaj te pola |
| | 2 | |
do siebie
12 paź 00:06
chichi:
Trójkąt czerwony jest równoboczny, ponieważ |∡DCB| = 60
o (to wiemy, ponieważ czworokąt ABCD
jest wpisany w okrąg) ∧ |BC| = 13
√3 = |CD|
12 paź 00:09
Kasia: 😘😘
12 paź 00:13
mat:
długość boku trójkąta równobocznego to 3√13 a nie 13√3
12 paź 00:13
Kasia: Mam jeszcze 2 zad których treści nie rozumiem
12 paź 00:14
chichi:
Wstaw w osobnych wątkach. @
mat skąd to spostrzeżenie?
12 paź 00:17
chichi:
Tak by wynikało z tw. Carnota. Ja nie sprawdzałem polecenia, ale rozwiązanie się nie zmieni
12 paź 00:18
chichi:
Przepisuj proszę zatem uważnie te polecenia bez
literówek
12 paź 00:18
Kasia: Pozostałe boki długości 13√3
Tak mam w poleceniu
12 paź 00:19
chichi:
To jest błąd, ponieważ nie zostałby nawet spełniony warunek istnienia trójkąta... Tw. Carnota
pokazuje, że bok ten powinien być długości 3
√13 jak napisał wyżej @
mat
12 paź 00:21
mat:
Przy takich danych, czworokąt nie istnieje
12 paź 00:43