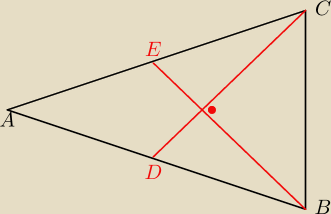
pole trójkąta lila: Dany jest trójkąt równoramienny ABC (AB=BC). Odcinki BE i CD są środkowymi poprowadzonymi z B i C do AC i AB. Wiedząc że BE ⊥ CD, BE=CD=12 oblicz pole trójkąta ABC.

janek191: Czy dobrze przepisana jest treść zadania?

wredulus_pospolitus: Na pewno nie jest dobrze przepisana treść zadania − takiego trójkąta nie można skonstruować.

an: 96 jaki problem

wredulus_pospolitus: @an taki, że mamy podane: |AB| = |BC|, a środkowe prowadzimy na AC i AB. W takim razie środkowa BE ⊥ AC. Skoro BE⊥ CD to znaczy, że AC ∥ CD. Narysuj mi trójkąt równoramienny w którym dwie (nie nakładające się) proste przechodzące przez jeden punkt są do siebie równoległe.

an: piszesz "W takim razie środkowa BE ⊥ AC" skąd to ma wynikać

janek191: @an: Ma być AB = BC.

an: Rzeczywiście

an: To jest ewidentny błąd powinno być AB=AC przemawia za tym reszta treści "Wiedząc, że (środkowe) BE ⊥ CD, BE=CD=12 oblicz pole trójkąta ABC" właściwie to zdanie jest wystarczające jako cała treść zadania.

wredulus_pospolitus: oczywiście, że tak winno być ... dlatego też było pytanie Janka i mój komentarz ... a reszta jest już historią