 8log21/2(x)−log31/2(x)≤20log1/2(x)−16
x>0
log1/2(x)=t
t3−8t2+20t−16≥0
t=2
1 −8 20 −16
1 −6 8 0
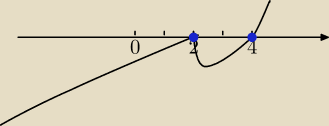
(t−2)*(t2−6t+8)=(t−2)* [(t−3)2−1)]=(t−2)*(t−3−1)*(t−3+1)=(t−2)2*(t−4)
t=2 lub t≥4
log1/2(x)=2 lub log1/2≥4
8log21/2(x)−log31/2(x)≤20log1/2(x)−16
x>0
log1/2(x)=t
t3−8t2+20t−16≥0
t=2
1 −8 20 −16
1 −6 8 0
(t−2)*(t2−6t+8)=(t−2)* [(t−3)2−1)]=(t−2)*(t−3−1)*(t−3+1)=(t−2)2*(t−4)
t=2 lub t≥4
log1/2(x)=2 lub log1/2≥4
| 1 | 1 | |||
x= | lub log1/2(x)≥log1/2 ( | )4 | ||
| 4 | 2 |
| 1 | ||
x≤ | ||
| 16 |
| 1 | 1 | |||
x∊(0, | >∪{ | } | ||
| 6 | 4 |
