Wskazac na plaszczyznie zespolonej zbiory liczb spelniajacych warunki: Niko: Wskazac na plaszczyznie zespolonej zbiory liczb spelniajacych warunki:

	π		π
1≤|z+2−i|≤3 i −		≤Argz≤
	3		3

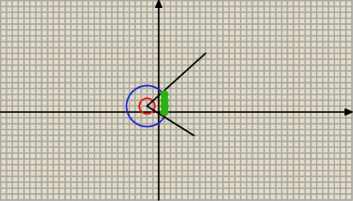
1≤|a+bi+2−i|≤3 1≤√(a+2)²+(b−1)²≤3 /(..)² 1≤(a+2)²+(b−1)²≤9 (a+2)²+(b−1)²≤9 (a+2)²+(b−1)²≥1 Wiem, że jest tu wzór na okrąg, ale nie wiem co dalej Narysowałem okrąg wraz z przedziałami, tylko nie wiem czy jest poprawny.

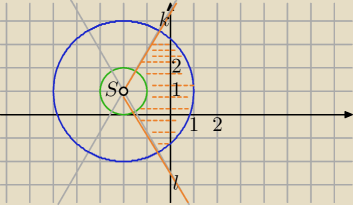
Mila: 1) 1≤|z−(−2+i)|≤3 pierścień o środku S=(−2,1) i r =1 (promień mniejszego okręgu) oraz R=r ( promień większego okręgu) i

	π		π
−		≤Arg(z)≤
	3		3

półproste zawierające się w prostych k il , gdzie: k: y=√3x +b 1=−2√3+b b=1+2√3 k: y=√3x+1+2√3 l: y=−√3x+1−2√3

ICSP: Argument liczby zespolonej wyznaczamy w odniesieniu do z = 0 a nie do liczby która jest środkiem pierścienia.

Mila: No widzisz, czyli Niko poprawi? To jest łatwiej , ja wyznaczyłam w stosunku to z₀=(−2+i)

ICSP: Moim zdaniem dobrze zaznaczył na swoim rysunku Kłóciłbym się z sformułowaniem "wzór na okrąg" dla układu nierówności: (a+2)²+(b−1)²≤9 (a+2)²+(b−1)²≥1 ale to jest już "szczegół".