Rozwiąż równanie, korzystając z p.algebraicznej - Liczby zespolone Niko: Rozwiąż równanie, korzystając z p.algebraicznej: 1) Rez−3Imz = 2 +3i Moje rozwiązanie: a−3bi=2+3i a=2 −3b=3 /(−3) a=2 b=−1 z=2−i Czy jest to poprawnie rozwiązane?

I'm back: z = x + iy Im(z) = y Re(z) = x L = x − 3y = 2 + 3i − − − bzdura a nie rownanie

Niko: Dlaczego?

I'm back: Dlatego że lewa strona jest liczba rzeczywista, a prawa urojona. Innymi słowy: x − y = 2 0i = − 3i <−−− i to jest totalna bzdura

Niko: Skoro: x − to część rzeczywista 2 − to w takim razie też rzeczywista 3y − to część urojona 3i − to też urojona Nie wystarczy tego do siebie porównać?

I'm back: 3y TO JEST LICZBA RZECZYWISTA

I'm back: Im(z) ∊ R (to być liczba rzeczywista)

Niko: Im(z) oznacza przecież część urojona liczby zespolonej

Mila: Lczby zespolone> https://www.matemaks.pl/definicja-liczby-zespolonej.html

I'm back: Zajrzyj do teorii. z = x + iy, zarówno x jak i y to liczby RZECZYWISTE iy to nie jest liczba rzeczywista Im(z) = y to być liczba rzeczywista

Niko: Czyli dopiero jak się pojawi "i" przy Y staję się to częścią urojoną

Niko: Mila: Właśnie tutaj jestem i myli mnie to, ze b oznacza część urojona, a jest jednak rzeczywistą

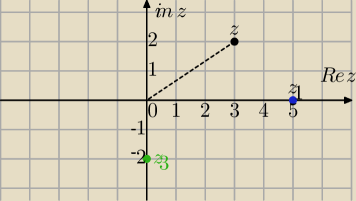
Mila: Niko, inaczej być nie może: z=3+2i, Re(z)=3 , Im(z)=2 z₁=5+0*i Re(z₁)=5, Im(z₁)=0 z₃=0−2i Re(z₃)=0, Im(z₃)=−2

Niko: A jak wykonać dalej to? |z−1−i|=1 |a+bi−1−i|=√([a−1]²+[b−1]²)=1

HGH: 3Imz możesz rozumieć jako 3* to co stoi (rzeczywiste) przy urojonej części liczby zespolonej z

wredulus_pospolitus: dalej [a−1]² + [b−1]² = 1 <−−− równanie okręgu o środku (1,1) i promieniu 1

Niko: Tylko, że to jest pod pierwiastkiem

wredulus_pospolitus: podnosisz do kwadratu

wredulus_pospolitus: i już pierwiastka ni ma