Nierówność z parametrem Pr713: Dobry wieczór, tutaj w tym zadaniu 1, pod tym linkiem https://forum.zadania.info/viewtopic.php?t=61892 Należy rozważyć dwa przypadki prawda? Gdy licznik jest dodatni a mianownik ujemny oraz gdy licznik jest ujemny a mianownik dodatni, co nie? Więc jest tutaj błąd w rozwiązaniu. Chodzi mi o same warunki gdyż nie zamierzam tego rozwiązywać.

Pr713: Oraz oczywiście jeszcze przypadek liniowy

ite: A nie lepiej zapytać na tamtym forum? Osoba, która odpowiadała, najlepiej wyjaśni, czym się kierowała. Zwłaszcza jak nie zamierzasz tego zadania rozwiązywać.

Pr713: Zapytać o post sprzed 7 lat?

Pr713: Już sam się namyśliłem i znam odpowiedź, nie zauważyłem że w mianowniku przy x² nie ma parametru więc może być tylko ≥ 0

wakacje:

(m+2)x2+x+m+2
	<0
x2−(m+5)x+9

f(x)=(m+2)x²+x+m+2 Δ_f=1−4(m+2)²=1²−(2m+4)²=(1+2m+4)(1−2m−4)=(2m+5)(−2m−3) g(x)=x²−(m+5)x+9 Δ_g=(m+5)²−36=(m+5)²−6²=(m+5−6)(m+5+6)=(m+11)(m−1) Z pewnością należy założyć, że Δ_g<0. Wtedy g(x)>0 dla x∊ℛ i możemy pomnożyć obustronnie nierówność przez mianownik (bez zmiany znaku nierówności) Otrzymujemy nierówność: (m+2)x²+x+m+2<0 A to jest z kolei spełnione, gdy: Δ_f<0 ∧ m+2<0 (i sprawdzić tak jak wspomniałeś, przypadek funkcji liniowej)

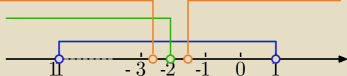
Mila: 1) Mianownik >0 dla m∊(−11,1) i 2) licznik ujemny dla każdego x∊R⇔ m+2<0 i Δ<0 ⇔ m<−2 i (−2m−3)*(2m+5)<0

	5		3
m<−2 i [m<−		lub m<−		]
	2		2

3) Odpowiedź:

	5
m∊(−11,−		)
	2

Funkcja liniowa y=x przyjmuje wartości dodatnie i ujemne , zatem odpada ta możliwość.

pr713: Tak wiem już − jak napisałem wyżej, −> funkcja w mianowniku nie ma parametru przy x², więc nie może mieć wartości tylko ujemnych − może mieć natomiast tylko dodatnie ( bo a > 0) dla Δ < 0 ⇔ m∊(−11,1) i x∊R, więc 2 przypadek nie ma miejsca gdy mianownik jest < 0 a licznik > 0

Mila: