proszę o rozwiązanie anna: Wyznacz wszystkie wartości parametru a , dla których równanie |x − 7| = (a + 2)² − 9 ma dwa różne rozwiązania dodatnie.

wakacje: |x−7|=(a+2)²−9 → założenie wynikające z wartości bezwzględnej, że (a+2)²−9>0 |x−7|=(a+2)²−9 x−7=(a+2)²−9 v x−7=−((a+2)²−9) x=(a+2)²−2 v x=−(a+2)²+16 Równanie ma mieć dwa różne rozwiązania dodatnie, zatem muszą być spełnione następujące warunki: 1) (a+2)²−2≠−(a+2)²+16 2) (a+2)²−2>0 3) −(a+2)²+16>0 4) (a+2)²−9>0 1) a∊ℛ\{−5,1} 2) a∊(−∞;−2−√2)∪(√2−2;+∞) 3) a∊(−6;2) 4) a∊(−∞;−5)∪(1;+∞) Część wspólna: a∊(−6;−5)∪(1;2)

anna: dziękuję

ite: czy w 4/ warunku (założenie wynikające z wartości bezwzględnej) nie powinna być nierówność nieostra?

wakacje : Czy wtedy równanie |x−7|=0 ma dwa różne rozwiązania?

ite: Spojrzałam na pierwszy wers, a warunek 4/ jest podany po informacji o dwóch różnych rozwiązaniach, więc moja uwaga jest zbędna.

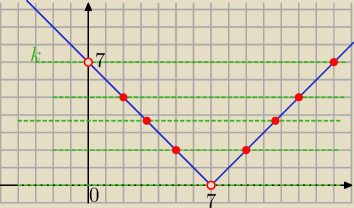
jesień: 2 sposób graficznie dwa rozwiazania dodatnie gdy k∊(0,7) k=(a+2)²−9 zatem (a+2)²−9>0 i (a+2)²−9<7 (a+2+3)(a+2−3)>0 i (a+2+4)(a+2−4)<0 a∊(−∞, −5)U(1,∞) i a∊(−6,2) część wspólna a∊(−6,−5) U (1,2)