proszę o rozwiązanie anna: Wierzchołki trójkąta ABC mają współrzędne: A = (− 6,3 ),B = (− 2,− 5),C = (3,0) . Okrąg o jest styczny do prostej AC , a jego środek jest punktem przecięcia się wysokości trójkąta ABC . Okrąg o przecina prostą BC w punkcie D ⁄= B . Oblicz iloraz |BD | : |DC | .

mat:

|BD|
	=4
|DC|

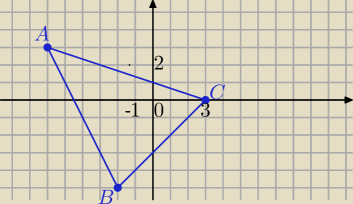
Mila: 1) Napisz równania : a) prostej AC, następnie prostej k do nie prostopadłej i przechodzącej przez punkt B b) prostej BC ,następnie prostej m do nie prostopadłej i przechodzącej przez punkt A c) Punkt przecięcia prostych k i m to będzie środek okręgu− S d) r− odległość punktu punktu S od prostej AC dalej poradzisz sobie?

anna:

	1
prosta AC to y= −		x + 1 k ⊥ prAC to y= 3x +1
	3

prosta BC to y = x − 3 m ⊥ pr BC to y = −x − 3 środek okręgu S = ( −1 ; −2 ) a promień r = √10 ale nie wiem jak obliczyć współrzędne punktu D

I'm back: Masz środek, masz promień − − możesz zapisać równanie okręgu. Przyrównujesz do rownania prostej BC pamiętając że D ≠ B. Z rysunku widać że D = ( 2, − 1)

anna: już wiem D = ( 2 ; −1) I DC I = √2 I BD I = √20 czyli

BD
	= √10 a nie jak napisał mat 2paż 20:46
DC

gdzie mam błąd

anna:

	BD
już znalazłam błąd stosunek		= 4
	DC

Mila: