zad
matthew: Cześć,
mam takie zadanie:
Przekształć do najprostszej postaci wyrażenie:
| | √2c2 | | a | | a | |
( |
| − |
| ) * |
| |
| | 4√2ac − a2 | | 4√2c − a | | a + 4√2c | |
Proszę o pomoc...
4 mar 16:30
matthew: Mam jeszcze takie zadanie:
Dane są funkcje liniowe g i h okreslone wzorami g(x) = ax+b oraz h(x) = bx + a.
Wiadomo, że funkcja g jest rosnąca, a funkcja h malejąca.
a) Wyznacz współrzędne punktu przeciecia wykresów tych funkcji.
b) Wyznacz liczby a i b wiedząc, że wykresy funkcji g i h prostymi prostopadłymi, a punkt ich
przecięcia leży na oso OX.
a) zrobiłem tak:
g(x) = ax+b (rosnąca) −−−−−−−−−−−− g(x) = x − b
h(x) = bx + a (malejąca) −−−−−−−−−−−−h(x) = − x + a
{y = x − b
{y = − x + a
−x + a = x − b
−2x = − b − a
2x = b + a
2y = b + a − 2b
2y = a − b
Bardzo proszę o sprawdznie...
Punktu b) nie potrafie zrobic... prosze o pomoc
4 mar 17:37
Godzio: narazie pierwsze pomagam
4 mar 17:58
Godzio: | | √2c2 | | a | | a | |
( |
| − |
| ) * |
| = |
| | 4√2ac−a2 | | 4√2c−a | | a+4√2c | |
| | √2c2 | | a2 | | a | |
( |
| − |
| ) * |
| = |
| | 4√2ac−a2 | | 4√2ac−a2 | | a+4√2c | |
| √2c2−a2 | | a | |
| * |
| = |
| a(4√2c−a) | | a+4√2c | |
| (4√2c−a)(4√2c+a) | | 1 | |
| * |
| = |
| 4√2c−a | | a+4√2c | |
4 mar 18:01
Godzio:
g(x) = ax + b
h(x) = bx + a
a>0
b<0
ax + b = bx + a
ax − bx = a − b
x(a−b) = a−b
x = 1
y = a+b
punkt przecięcia: A(1, a+b )
b)
g(x) = ax + b
h(x) = bx + a
proste prostopadłe:
0 = ax + b
0 = bx + a ich punkt wspólny znajduje się na OX więc B(x,0)
0 = −x + b
2
0 = b
2x − 1
x = b
2
0 = b
4 − 1
0 = (b
2−1)(b
2+1)
0 = (b−1)(b+1)(b
2+1)
b = 1 v b = −1
wiemy że :
a>0
b<0
więc b = −1 a = 1
4 mar 18:07
matthew: Dzieki
Godzio 
Nie rozumiem jednej rzeczy... tzn. z jakiej własności skorzystałeś w tej drugiej linijce
pierwszego zadania. Nagle obydwa mianowniki w nawiasie są identyczne.... jak to zrobiłeś?

Są tutaj podobne zadanie, jak to pierwsze ?
4 mar 18:24
Godzio: jeśli chodzi o pierwsze to sprowadziłem do wspólnego mianownika, a czy są to tego już nie wiem

trzeba by było poszperać

4 mar 18:46
matthew: ok

mam jeszcze takie zadanie:
Wiedząc, że |x − 1| ≤ 3 oraz |y + 3| ≤ 5, wyznacz najwiekszą i najmniejszą wartość iloczynu xy.
zacząłem tak:
− 3 ≤ |x − 1| ≤ 3
− 3 ≤ |x − 1| ∧ |x − 1| ≤ 3
x ≥ − 2 x ≤ 4
x ∊ <−2; 4>
−5 ≤|y + 3| ≤ 5
−5 ≤|y + 3| ∧ |y + 3| ≤ 5
y ≥ − 8 y ≤ 2
y ∊ <− 8; 2>
Iloczyn to część wspólna?
Bo jeżeli tak, to:
xy ∊ < −2; 2>
i nie wiem co dalej.... tzn. próbowalem narysować dwa wykresy... czyli wyznmaczałem:
y
1 = x − 1
y
2 = |x−1|
y
3 = |x − 1| − 3
ale nie wiedzialem jak zabrac sie za to drugie wyrażenie....
Proszę o pomoc
4 mar 19:03
Godzio: ja bym zrobił dokładnie tak jak ty tyle że odpowiedź już jest tutaj:
xy∊ <−2,2>
największa : 2
najmniejsza −2
tak mi się wydaje

4 mar 19:06
matthew: ... kurcze.. no własnie nie...
mam do tego zadania odpowiedz: m = − 32; M = 16
4 mar 19:20
Godzio: y ∊ <−8,2>
x ∊ <−2,4>
max wartość to najmniejsza wartość y i najmniejsza x => −8*(−2) = 16
minimum: najmniejsza y * największa x => −8 * 4 = −32

4 mar 19:24
matthew: ok. rozumiem to co napisałeś, tzn. te dwa zdania są zgodne z Twoimi obliczeiami, ale skąd
wziąłeś taką własność? .... ech wiele razy obliczałem wartość max i min., ale z takim
podejsciem jeszcze sie nie spotkałem....
4 mar 19:41
Godzio: wsumie to nie wiem, na logike, iloczyn koncow przedzialow da nam najwieksza i najmniejsza
wartosc nie zabardzo wiem jak to wyjasnic

4 mar 19:47
Bogdan:
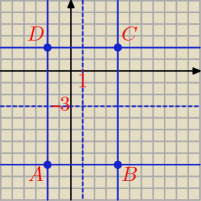
|x − 1| ≤ 3 ⇒ −2 ≤ x ≤ 4
|y + 3| ≤ 5 ⇒ −8 ≤ y ≤ 2
A = (−2, −8), −2 * (−8) = 16, M = 16
B = (4, −8), 4 * (−8) = −32, m = −32
C = (4, 2), 4 * 2 = 8
D = (−2, −2), −2 * (−2) = 4
4 mar 20:21
matthew:

Mam takie zadanie:
Dany jest trójkąt ABC, jak na rysunku, gdzie O oznacza środek okręgu wpisanego w ten trójkąt.
Wyznacz miary kątów wewnętrznych tego trójkąta.
1 = 120
O
2 = 110
O
3 = 130
O
Z jakich własności należy tutaj skorzystać? Nie wiem jak sie zabrac za to zadanko
Proszę o pomoc...
4 mar 21:02
Bogdan:
Trzeba skorzystać z;
1. suma miar kątów wewn. trójkąta = 180o.
2. środek okręgu wpisanego w trójkąt jest punktem przecięcia ...
4 mar 21:12
Godzio:
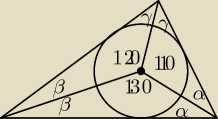
środek okręgu wpisanego w trójkąt wyznaczają dwusieczne kątów

β + α + 130 = 180
β + γ + 120 = 180
γ + α + 110 = 180
β + α = 50
β + γ = 60
γ + α = 70
β = 50 − α
γ = 70 − α
50 − α + 70 − α = 60
2α = 60
α = 30
γ = 70 − 30 = 40
β = 50 − 30 = 20
4 mar 21:15
matthew:
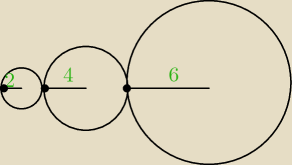
mam jeszcze takie zadanie:
Trzy okręgi o promieniach 2, 4, 6 są parami zewnętrznie styczne. Oblicz długośc promienia
okręgu przechodzącego przez punkty styczności tych okręgów.
no i nie wiem.... to ma wyglądać tak jak na rysunku?

srdenica okręgu o promieniu 2 wynosi 4, sr. okr. o promieniu 4 = 8, sr. okr. o promieniu 6 = 12
wiec po prostu moglbym dodac te srednice i wyszedlby mi promien przechodzacy przez każdy z
punktów przecięcia....
ale to byloby zbyt banalne, zeby było prawdziwe...

Prosze o pomoc...
4 mar 21:17
Eta:
Pomagam

.....rysuję
4 mar 21:30
Eta:
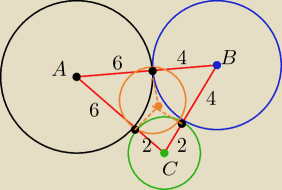
Przepraszam , ale chwilowo musiałam odejść od komputera

IABI= 10 IACI= 8 IBCI= 6
trójkąt ABC jest prostokatny
bo 10
2= 8
2 +6
2
| | 6+8+10 | |
P= 12*6*8 = 24 p= |
| = 12
|
| | 2 | |
r
wp=2 [j]
4 mar 21:54
matthew: Mam jeszcze takie zadanie:
Uzasadnij, że wariancja wszystkich wyrazów dowolnego skończonego ciągu liczbowego stałego równa
jest zero.
Dziekuje za odpowiedzi

4 mar 23:31
Sabin:
Srednia wyrazow ciagu stalego rowna jest jego dowolnemu wyrazowi:
ciag: 5,5,5,5,5 − srednia 5.
stad, xsr = x
Skorzystamy z troche innego niz zwykle wzoru na wariancje:
σ2 = 1n∑xi2 − (xsr)2
wszystkie xi sa takie same i rowne x. Wtedy ∑xi2 = nx2
Stad:
σ2 = 1nnx2 − x2 = 0.
A na ludzki jezyk: skoro wariancja wyraza odchylenia od sredniej, to poniewaz dla ciagu
stalego nie ma odchylen od sredniej (wszystkie wyrazy sa jej rowne), to musi wynosic 0.
4 mar 23:38
4 mar 23:44
matthew: Aha, czyli np
niech bedzie te 5 piątek,. srednia = 5
mozna to zapisac w ten sposob?
| | (5−5)2 + (5−5)2 + (5−5)2 + (5−5)2 + (5−5)2 | |
σ = |
| = 0 ? |
| | 5 | |
czyli ten dowolny, skonczony ciag liczbowy stalu, to np. 6 6 6 6 6; ?
4 mar 23:57
Sabin:
Tak, jak najbardziej mozna tez z tego wzoru, tylko oczywiscie zamiast liczb trzeba to
napisac bardziej ogolnie, czyli kolokwialnie mowiac, "na iksach".
5 mar 00:08
krupa: 1/x−1/y=1/z wspólny mianownik
13 gru 16:13
 Nie rozumiem jednej rzeczy... tzn. z jakiej własności skorzystałeś w tej drugiej linijce
pierwszego zadania. Nagle obydwa mianowniki w nawiasie są identyczne.... jak to zrobiłeś?
Nie rozumiem jednej rzeczy... tzn. z jakiej własności skorzystałeś w tej drugiej linijce
pierwszego zadania. Nagle obydwa mianowniki w nawiasie są identyczne.... jak to zrobiłeś?  Są tutaj podobne zadanie, jak to pierwsze ?
Są tutaj podobne zadanie, jak to pierwsze ?
 trzeba by było poszperać
trzeba by było poszperać
 mam jeszcze takie zadanie:
Wiedząc, że |x − 1| ≤ 3 oraz |y + 3| ≤ 5, wyznacz najwiekszą i najmniejszą wartość iloczynu xy.
zacząłem tak:
− 3 ≤ |x − 1| ≤ 3
− 3 ≤ |x − 1| ∧ |x − 1| ≤ 3
x ≥ − 2 x ≤ 4
x ∊ <−2; 4>
−5 ≤|y + 3| ≤ 5
−5 ≤|y + 3| ∧ |y + 3| ≤ 5
y ≥ − 8 y ≤ 2
y ∊ <− 8; 2>
Iloczyn to część wspólna?
Bo jeżeli tak, to:
xy ∊ < −2; 2>
i nie wiem co dalej.... tzn. próbowalem narysować dwa wykresy... czyli wyznmaczałem:
y1 = x − 1
y2 = |x−1|
y3 = |x − 1| − 3
ale nie wiedzialem jak zabrac sie za to drugie wyrażenie....
Proszę o pomoc
mam jeszcze takie zadanie:
Wiedząc, że |x − 1| ≤ 3 oraz |y + 3| ≤ 5, wyznacz najwiekszą i najmniejszą wartość iloczynu xy.
zacząłem tak:
− 3 ≤ |x − 1| ≤ 3
− 3 ≤ |x − 1| ∧ |x − 1| ≤ 3
x ≥ − 2 x ≤ 4
x ∊ <−2; 4>
−5 ≤|y + 3| ≤ 5
−5 ≤|y + 3| ∧ |y + 3| ≤ 5
y ≥ − 8 y ≤ 2
y ∊ <− 8; 2>
Iloczyn to część wspólna?
Bo jeżeli tak, to:
xy ∊ < −2; 2>
i nie wiem co dalej.... tzn. próbowalem narysować dwa wykresy... czyli wyznmaczałem:
y1 = x − 1
y2 = |x−1|
y3 = |x − 1| − 3
ale nie wiedzialem jak zabrac sie za to drugie wyrażenie....
Proszę o pomoc



 |x − 1| ≤ 3 ⇒ −2 ≤ x ≤ 4
|y + 3| ≤ 5 ⇒ −8 ≤ y ≤ 2
A = (−2, −8), −2 * (−8) = 16, M = 16
B = (4, −8), 4 * (−8) = −32, m = −32
C = (4, 2), 4 * 2 = 8
D = (−2, −2), −2 * (−2) = 4
|x − 1| ≤ 3 ⇒ −2 ≤ x ≤ 4
|y + 3| ≤ 5 ⇒ −8 ≤ y ≤ 2
A = (−2, −8), −2 * (−8) = 16, M = 16
B = (4, −8), 4 * (−8) = −32, m = −32
C = (4, 2), 4 * 2 = 8
D = (−2, −2), −2 * (−2) = 4
 Mam takie zadanie:
Dany jest trójkąt ABC, jak na rysunku, gdzie O oznacza środek okręgu wpisanego w ten trójkąt.
Wyznacz miary kątów wewnętrznych tego trójkąta.
1 = 120O
2 = 110O
3 = 130O
Z jakich własności należy tutaj skorzystać? Nie wiem jak sie zabrac za to zadanko
Proszę o pomoc...
Mam takie zadanie:
Dany jest trójkąt ABC, jak na rysunku, gdzie O oznacza środek okręgu wpisanego w ten trójkąt.
Wyznacz miary kątów wewnętrznych tego trójkąta.
1 = 120O
2 = 110O
3 = 130O
Z jakich własności należy tutaj skorzystać? Nie wiem jak sie zabrac za to zadanko
Proszę o pomoc...
 środek okręgu wpisanego w trójkąt wyznaczają dwusieczne kątów
środek okręgu wpisanego w trójkąt wyznaczają dwusieczne kątów  β + α + 130 = 180
β + γ + 120 = 180
γ + α + 110 = 180
β + α = 50
β + γ = 60
γ + α = 70
β = 50 − α
γ = 70 − α
50 − α + 70 − α = 60
2α = 60
α = 30
γ = 70 − 30 = 40
β = 50 − 30 = 20
β + α + 130 = 180
β + γ + 120 = 180
γ + α + 110 = 180
β + α = 50
β + γ = 60
γ + α = 70
β = 50 − α
γ = 70 − α
50 − α + 70 − α = 60
2α = 60
α = 30
γ = 70 − 30 = 40
β = 50 − 30 = 20
 mam jeszcze takie zadanie:
Trzy okręgi o promieniach 2, 4, 6 są parami zewnętrznie styczne. Oblicz długośc promienia
okręgu przechodzącego przez punkty styczności tych okręgów.
no i nie wiem.... to ma wyglądać tak jak na rysunku?
mam jeszcze takie zadanie:
Trzy okręgi o promieniach 2, 4, 6 są parami zewnętrznie styczne. Oblicz długośc promienia
okręgu przechodzącego przez punkty styczności tych okręgów.
no i nie wiem.... to ma wyglądać tak jak na rysunku?  srdenica okręgu o promieniu 2 wynosi 4, sr. okr. o promieniu 4 = 8, sr. okr. o promieniu 6 = 12
wiec po prostu moglbym dodac te srednice i wyszedlby mi promien przechodzacy przez każdy z
punktów przecięcia....
ale to byloby zbyt banalne, zeby było prawdziwe...
srdenica okręgu o promieniu 2 wynosi 4, sr. okr. o promieniu 4 = 8, sr. okr. o promieniu 6 = 12
wiec po prostu moglbym dodac te srednice i wyszedlby mi promien przechodzacy przez każdy z
punktów przecięcia....
ale to byloby zbyt banalne, zeby było prawdziwe...  Prosze o pomoc...
Prosze o pomoc...
 .....rysuję
.....rysuję
 Przepraszam , ale chwilowo musiałam odejść od komputera
Przepraszam , ale chwilowo musiałam odejść od komputera  IABI= 10 IACI= 8 IBCI= 6
trójkąt ABC jest prostokatny
bo 102= 82 +62
IABI= 10 IACI= 8 IBCI= 6
trójkąt ABC jest prostokatny
bo 102= 82 +62
