proszę o rozwiązanie anna: Okrąg jest styczny do osi układu współrzędnych w punktach A = (0,2) i B = (−2 ,0) oraz jest styczny do prostej l w punkcie C = (− 1,a) , gdzie a > 1 . Wyznacz równanie prostej l . wyznaczyłam środek okręgu S = (2 ; −2 ) i promieniu r =2 ( x−2)² + ( y +2) =4 podstawiłam za x = −1 i wtedy równanie nie ma rozwiązania jaki jest błąd

Kacper: Błędnie środek wyznaczony.

anna: słusznie ma być ( x+2)² + ( y −2)² =4

anna: prosta l ma równanie y =√3 x + 2√3 +2 proszę o sprawdzenie

ICSP: C(−1 , 2 + √3) (ponieważ a > 1) Prosta styczna: l : Ax + By + C = 0 1^o C ∊ l −A + B(2 + √3) + C = 0 ⇒ C = A − B(2 + √3) l : Ax + By + A − B(2 + √3) 2^o Odległość prostej od środka okręgu jest równa promieniowi:

	|−2A + 2B + A − B(2 + √3)|
2 =
	√A2 +B2

2√A² + B² = |A + B√3| 4A² + 4B² = A² + 2AB√3 + 3B² 3A² − 2AB√3 + B² = 0 (√3A − B)² = 0 B = √3A l: Ax + √3Ay + A − √3A(2 + √3) = 0 x + √3y + 1 − 2√3 − 3 = 0 x + √3y − 2 − 2√3 = 0

ICSP: prosta y = √3x + 2√3 + 2 co prawda przechodzi przez punkt C, ale jest rosnąca Co oznacza, że nie jest ona styczną tylko średnicą tego okręgu (przez środek też przechodzi)

ICSP: Średnica okręgu zawiera się w tej prostej*

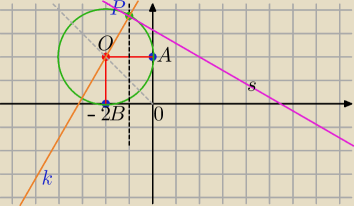
Iryt: (x+2)²+(y−2)²=2² 1) Punkt styczności: (−1+2)²+(y−2)²=4 (y−2)²=3 y−2=√3 lub y−2=−√3 y=√3+2 >1 lub y=−√3+2<1 C=(−1,√3+2) 2) Równanie stycznej do okręgu w punkcie C∊okręgu: k: y=√3x+√3+2 − sieczna przechodząca przez punkty O i C Styczna: s⊥k

	1
y=−		x+b
	√3

	√3		2√3
y=−		x+		+2
	3		3

anna: dziękuję