obraz Waksma: Znajdź obraz krzywej f(x)=x+sinx względem prostej y+x=0

M:

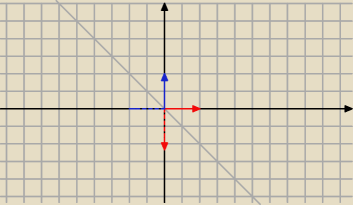
Maciess: Skorzystamy z tego, że odbicie wzlędem prostej jest p. liniowym. Znajdżmy wzór na odbicie względem tej prostej dla dowolnego punktu, a potem wstawmy tam wzór naszej funkcji. Znajdzmy macierz przekształcenia patrząc na co przechodzą wektory bazy standardowej R². Z obrazka odczytamy, że

1 0		0 −1
	→

0 1		−1 0
	→

	0 −1 −1 0
Mamy więc macierz przekształcenia postaci A =

	x x+sin(x)
Krzywa możemy sparametryzować dla x

	x x+sin(x)		−(x+sinx) −x
Więc obraz krzywej to bedzie Ax = A		=

No to juz nam daje parametryzacje. Żeby lepiej zrozumieć fajnie przedstawić to przekształcenie jako złożenie przekształcen. W geogebrze rysuneczek ze sprawdzeniem https://www.geogebra.org/calculator/mvr26adk