zbiór wartości dobromil: Cześć, proszę o pomoc, jak wyznaczyć zbiór wartości takiej funkcji? f(x)=−|(¹₄)^2−x+3|

wakacje:

	1
f(x)=−|(		)2−x+3|, x∊R
	4

	1		1		1
zauważmy na początku, że (		)2−x=(		)4−2x=22x−4=22x*2−4=		*4x
	4		2		16

wyjdziemy od zbioru wartości podstawowej funkcji i będziemy kolejno przekształcać

	1
f(x)=−|		*4x+3|
	16

1) f(x)=4^x → ZW: (0;+∞)

	1
2) f(x)=		*4x → ZW: (0;+∞)
	16

	1
3) f(x)=		*4x+3 → ZW: (3;+∞)
	16

	1
4) f(x)=|		*4x+3| → ZW: (3;+∞)
	16

	1
5) f(x)=−|		*4x+3| → ZW: (−∞;−3)
	16

paweł: Rozumiem juz, bardzo Ci dziękuję, na początku chciałem wyliczać a wystarczyło z przekształceń. Dzięki, dobrej nocy!

wakacje: wyliczać też można, ale trochę więcej zabawy i nie wiem czy wszystkie kroki byłyby u mnie potrzebne wyznaczmy takie m, dla których równanie f(x)=m ma rozwiązanie: f(x)=m

	1
−|		*4x+3|=m
	16

	1
|		*4x+3|=−m (warunek wynikajacy z wartości bezwzględnej, że m<0)
	16

1		1
	*4x+3=−m v		*4x+3=m
16		16

4^x=−16(m+3) v 4^x=16(m−3) Teraz założenie wynikające ze zbioru wartości funkcji g(x)=4^x [−16(m+3)>0 ∧ 16(m−3)>0] v [−16(m+3)>0 ∧ 16(m−3)<0] v [−16(m+3)<0 ∧ 16(m−3)>0] (m<−3 ∧ m>3) v (m<−3 ∧ m<3) v (m>−3 ∧ m>3) m∊∅ v m<−3 v m>3 m∊(−inf;−3)∪(3;+inf) ∧ m<0 m∊(−inf;−3) próbowałbym chyba w ten sposób

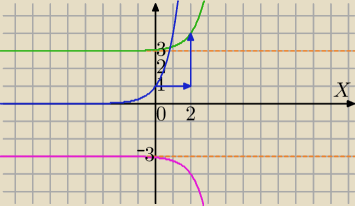
Iryt: Graficznie: f(x)=−|4^x−2+3| 1) g(x)=4^x→T_[2,3]⇒h(x)=4^x−2+3=|4^x−2+3| bo 4^x−2+3>0 h(x)→S_OX⇒f(x)=−|4^x−2+3| Zw_f=(−∞,−3) 2) Równanie : f(x)=m ma rozwiązanie dla m<−3