Pole równoległoboku Mila: Niech ABCD będzie równoległobokiem z BC = 5, i M jest punktem na boku CD takim, że MC: MD = 4: 3. Załóżmy, że BM, AM są prostopadłe do AC, BD odpowiednio. Oblicz pole ABCD.

chichi: Jak to załóżmy, że są? Albo są albo nie, dziwne polecenie

Mila: Właśnie taka treść

chichi: A z jakiego zbioru/podręcznika zadanie pochodzi jeśli można wiedzieć?

Kacper: Czy to pole to 7√24?

an: To jest najprawdopodobniej prawidłowy wynik mnie z symulacji wyszło ≈34,2928564, a bok 7,0000000

chichi: Tak wynik jest poprawny, ale 7√24 = 14√6

Mila: To jest zadanie z forum, napisał to użytkownik miki.

chichi: W końcu się doczekałem, wynik u góry

Kacper: Ciekaw jestem waszych pomysłów na rozwiązanie, bo wynik znam, ale już prosty sposób na rozwiązanie to średnio.

chichi: Prosty sposób wymaga dużo obliczeń, szybki sposób − sprytu i wiedzy, o którym mówisz?

Kacper: Najlepiej oba, rozwiązania za zwyczaj są inspirujące

Kacper: *zazwyczaj

www: https://www.quora.com/Let-ABCD-be-a-parallelogram-with-BC-5-and-M-is-the-point-on-the-side-CD-such-that-MC-MD-4-3-Suppose-that-BM-and-AM-are-perpendicular-to-AC-and-BD-respectively-What-is-the-area-of-ABCD

Kacper: Ciekawe, ale rozwiązania bardziej typu olimpijskiego trochę 🤔

chichi: Takie najlepsze, ale to i tak nieco przekombinowane

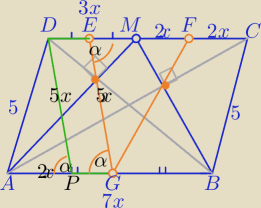
Mila: 1) Odcinek łączący środki podstaw trapezu przechodzi przez punkt przecięcia jego przekątnych.

	11x
2) |EG|=5x, |FG|=		, |PD|=5x
	2

	1
3) W ΔEGF: cosα=		z tw. sinusów
	5

	1
4) W ΔAPD: 52=4x2+25x2−2*2x*5x *		⇔x=1
	5

5) ΔAPD− Δrównoramienny: 5,5,2 h²=24 P_ABCD=7*2√6=14√6 Jeżeli Kacper widzisz prostszy sposób to napisz wskazówkę (własność, której nie widzę).