Trójkąt, pole, równoległobok
Szkolniak: Wykazać, że trójkąt wpisany w równoległobok ma co najwyżej połowę pola powierzchni
równoległoboku.
| | 1 | |
Mamy do wykazania nierówność PΔ≤ |
| Prówn |
| | 2 | |
Kąt ostry w równoległoboku oznaczę jako alfa, gdzie α∊(0
o;90
o)
Po przekształceniach tej nierówności dochodzę do tego że mam wykazać prawdziwość nierówności
sin(α)≥0, co jest prawdą dla α∊(0
o;90
o)
Czy mogę to uznać za zakończenie dowodu?
Jeśli za mało szczegółowo i potrzeba opisu, to chętnie przedstawię swoje rozwiązanie
20 wrz 18:18
chichi:
Czyli jednym słowem − coś dowodzisz, przekształcasz, a nawet nie wiesz co?

20 wrz 18:45
chichi:
Dlaczego wykluczamy możliwość przyjmowania przez alfę miary 90
o?

20 wrz 18:46
Szkolniak: Jak to nie wiem co? Po prostu doszedłem do takiej postaci nierówności, ale może rzeczywiście
przedstawię całe swoje rozwiązanie, bo tak naprawdę nie wiadomo o co ja pytam ani jak mi
odpowiedzieć. Może komuś będzie chciało się prześledzić mój tok rozumowania.
20 wrz 19:04
Mariusz:
sin(α)≥0 to akurat jest prawdą dla α∊[0°;180°]
20 wrz 19:08
chichi:
Ja po prostu nie rozumiem Twoich wątpliwości co do prawdziwości tej nierówności dla zadanej
alfy, o ile ta nierówność jest równoważna tej wyjściowej

20 wrz 19:08
Szkolniak:
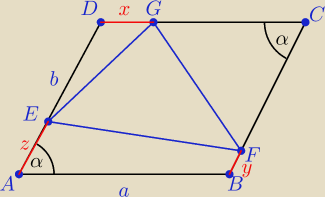
P − pole równległoboku ABCD, α∊(0
o;90
o>
|DG|=x ⇒ |GC|=a−x
|BF|=y ⇒ |CF|=b−y
|AE|=z ⇒ |ED|=b−z
(1) P=absin(α)
(2) P
ΔEFG=P−P
ABFE−P
ΔFCG−P
ΔGDE
| | 1 | | x(b−z) | |
PΔGDE= |
| *x*|ED|*sin(180o−α)= |
| *sin(α) |
| | 2 | | 2 | |
| | 1 | | (a−x)(b−y) | |
PΔFCG= |
| *|GC|*|CF|*sin(α)= |
| *sin(α) |
| | 2 | | 2 | |
Pole P
ABFE obliczymy w ten sposób, że prowadzimy prostą EH, gdzie H∊BC, która jest
równoległa do prostej AB.
W ten sposób powstaje nam równoległobok ABHE.
|AE|=|BH|=z ⇒ z=|BF|+|FH|, z=y+|FH| ⇒ |FH|=z−y
| | 1 | |
PABFE=PABHE−PΔEFH=azsin(α)− |
| a(z−y)sin(α) |
| | 2 | |
| | 1 | | x(b−z) | | (a−x)(b−y) | |
(4) PΔEFG=absin(α)−azsin(α)+ |
| a(z−y)sin(α)− |
| *sin(α)− |
| *sin(α) |
| | 2 | | 2 | | 2 | |
(5) Udowadniamy nierówność:
2P
ΔEFG≤P
2absin(α)−2azsin(α)+a(z−y)sin(α)−x(b−z)sin(α)−(a−x)(b−y)sin(α)≤absin(α)
sin(α)[2ab−2az+a(z−y)−x(b−z)−(a−x)(b−y)−ab]≤0
sin(α)(xz−az−xy)≤0
sin(α)(xy+z(a−x))≥0
(x>0 ∧ y>0) ⇒ xy>0
(z>0 ∧ a−x>0) ⇒ z(a−x)>0
(xy>0 ∧ z(a−x)>0) ⇒ xy+z(a−x)>0
sin(α)(xy+z(a−x))≥0 |:(xy+az−xz)
sin(α)≥0, co jest prawdą dla a∊(0
o;90
o>, cnw.
20 wrz 19:52
Maciess: A pamiętasz wzór na pole równoległoboku rozpiętego przez dwa wektory? A jak on wygląda dla
trojkąta rozpiętego przez tą sama dwójke? Może łatwiej (szybciej i czytelniej) byłoby
uzasadnić kiedy trójkąt wpisany będzie największy?
20 wrz 21:48
Mila:
Wykaż, że ze środkowych dowolnego trójkąta można zbudować trójkąt.
20 wrz 22:24
Mila:
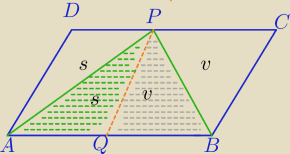
Ad zad.1)
Jeśli punkt P należy do boku DC równoległoboku ABCD to
Dowód.
Prosta PQ||AD dzieli ABCD na dwa równoległoboki.
Trójkąt ABP utworzony jest z ich połówek.
20 wrz 22:57
chichi:
| | 1 | | 1 | |
Niech d(P, AB) = h, wówczas: [ABP] = |
| *|AB|*h = |
| [ABCD]  |
| | 2 | | 2 | |
20 wrz 23:09
Mila:
Jasne, to każdy wie, ale taki podział jak pokazałam przydaje się w innych zadaniach.
20 wrz 23:24
chichi:
Pewnie, masz jakieś ciekawe zadanie z równoległobokiem? Dawno nie działałem z tą figurą

20 wrz 23:35
kerajs:
Gdyby na grafice z 19:52 dodać sieczną równoległą do boku równoległoboku i przechodzącą przez E
(lub G) to w otrzymanych równoległobokach fragmenty trójkąta są mniejsze od połowy pól tych
równoległoboków.
Obawiam się, że taki dowód wystarczyłby chichi, jednak dla nauczycieli (w tym i sprawdzjących
egzaminy), dziwny i niezrozumiały (i niezasługujący na max),.
21 wrz 00:25
Szkolniak: Dlaczego możemy przyjąć, że podstawa trójkąta zawiera się w boku równoległoboku? Nie powinniśmy
przyjąć bardziej niesprecyzowanego umieszczenia tego trójkąta?
21 wrz 00:58
Mila:
Szkolniak podałam 22: 57 informację , aby wykorzystać do dowodu ikonicznego.
Tam masz Δ o największym polu.
22:24 masz inne zadanie− można wykazać bez rachunków.
21 wrz 16:57



 P − pole równległoboku ABCD, α∊(0o;90o>
|DG|=x ⇒ |GC|=a−x
|BF|=y ⇒ |CF|=b−y
|AE|=z ⇒ |ED|=b−z
(1) P=absin(α)
(2) PΔEFG=P−PABFE−PΔFCG−PΔGDE
P − pole równległoboku ABCD, α∊(0o;90o>
|DG|=x ⇒ |GC|=a−x
|BF|=y ⇒ |CF|=b−y
|AE|=z ⇒ |ED|=b−z
(1) P=absin(α)
(2) PΔEFG=P−PABFE−PΔFCG−PΔGDE
 Ad zad.1)
Jeśli punkt P należy do boku DC równoległoboku ABCD to
Ad zad.1)
Jeśli punkt P należy do boku DC równoległoboku ABCD to

