15 wrz 20:18
I'm back:
Kat ADB = 180 − 80 − x = 100 − x
Ale także kat ADB = 180 − 20 − 2x = 160 − 2x
Stad x = 60o
I teraz parę tw. cosinusa i da się to wyciagnac
15 wrz 20:24
chichi:
Trochę dookoła żeś poleciał
ΔABC: 20
o+30
o+70
o+x=180
0 ⇒ x=60
o
15 wrz 20:28
chichi:
P.S. Odpuściłbym sobie 'parę tw. cosinusa'
15 wrz 20:30
pomocyy: A do których trójkątów zrobić to tw. cosinusa?
15 wrz 20:37
pomocyy: halo
15 wrz 22:02
chichi:
|BC| = 2
√3
15 wrz 22:29
pomocyy: Poprosiłam pana i dał mi czas do jutra na zrobienie tego
16 wrz 14:34
pomocyy: A sam wynik niestety mnie nie ratuje
16 wrz 14:37
chichi:
A co sam zrobiłeś, do czego doszedłeś, co już wyliczyłeś?
16 wrz 15:45
a7: chętnie bym pomogła, ale sama nie umiem dojść do tego wyniku, a @chichi na razie nie dal
żadnych naprowadzeń podpowiedzi, wskazówek, z tw, cosinusów też nie wiem jak tu skorzystać
może jeszcze ktoś coś pomoże
16 wrz 19:35
pomocyy: Ja też trochę poukładałam ale chyba na marne nic z tego nie mogę wyciągnąć
16 wrz 20:09
Szkolniak: Ja jestem w stanie stworzyć układ 6 równań z sześcioma niewiadomymi, więc niby by szło to
wyliczyć. Pomyślę jeszcze nad jakimś innym sposobem
16 wrz 20:36
pomocyy: To zadanie pochodzi z działu planimetria myślę że tutaj trzeba coś może dorysować tylko co?
16 wrz 20:43
chichi:
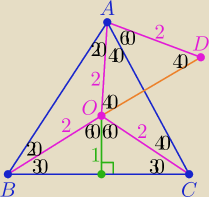
|BC| = 2
√3
16 wrz 20:57
pomocyy: Wow jak na to wpadłeś?
16 wrz 21:28
chichi:
Tak przez przypadek...
Jutro wstawię drugie rozwiązanie, dziś mi się nie chce już rysować...
17 wrz 00:24
a7: o fajnie
17 wrz 01:31
chichi:
@
a7 fajnie, że pojawiło się rozwiązanie czy, że wstawię drugie? Dobrej nocy
17 wrz 01:36
Mila:
a7
1)tw. sinusów w ΔABD, BD=AC+2
2) tw. sinusów w ΔABC
3) Porównać AC, wynik można zostawić albo pomęczyć się i otrzymasz długość BC jak u
chichi.
17 wrz 19:43
chichi:
@
Mila to super, że wyniki takie same. Ale autorka chyba potrzebowała tylko żeby ktoś
rozwiązał jej zadanie domowe... Masz jakiś inny pomysł nieco bardziej syntetyczny? Mam jeszcze
jedno fajne rozwiązanie ale wrzucę je jutro, to możesz wrócić I rzucić okiem
17 wrz 19:57
a7:
@
Mila Dziękuję
!
@
chichi jedno i drugie, fajnie , że pojawiło się rozwiązanie, które jestem w stanie
zrozumieć, a jak będzie drugie to w sumie też fajnie
17 wrz 21:18
chichi:
@
a7 jakby pojawiły się jakieś pytania, to śmiało wal, z miłą chęcią na nie odpowiem
Kto pyta nie błądzi, czy jakoś tak..
17 wrz 23:08
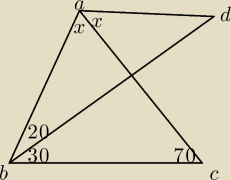Korzystając z rysunku wyznacz długość BC, jeśli dłg. AD wynosi 2 oraz BD=AD+AC. Ponadto miary
kątów ABD, DBC oraz BCA wynoszą odpowiednio 20, 30 i 70 stopni, a AC jest dwusieczną kąta BAD.
Siedzę nad tym już z 2h pomocy