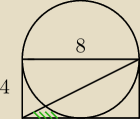
pole 123: Oblicz pole zielonej części prostokąta.

kerajs: Dolny trójkąt = zielone pole + odcinek koła + trójkąt krzywoliniowy

1		1		1
	4*8=X+		42(π−2arcctg2−sin (2arcctg2))+(42−		π42)
2		2		4

Szkolniak:

	256		3		3
Mi pole wyszło równe P=		−4sin(2arcsin(−		))−8arcsin(−		), nie sprawdzałem
	25		5		5

czy to równe tyle, co u kerajsa.

Szkolniak: Tak swoją drogą, jeśli dobrze liczę, Twoje pole kerajs wychodzi ujemne, czy może tak być?

Szkolniak: Jednak jest ono dodatnie, więc źle powiedziałem. Też zacząłem wątpić w swój sposób rozwiązania tego zadania.. Bo ogólnie miałem taki pomysł aby całe zadanie osadzić w układzie współrzędnych i zrobiłem to za pomocą całek, ale z tego co widzę to końcowy wynik zależy od tego, w którym dokładnie miejscu osadzimy te dwie figury Gdyby ktoś był chętny to w sumie mogę wrzucić skan rozwiązania z zeszytu, może ktoś rzuci okiem

kerajs: 1. Ujemne pole wskazuje na popełniony gdzieś błąd. 2. Wynik powinien być taki sam, niezależnie od umiejscowienia figury w układzie współrzędnych. 3. Mogę sprawdzić rozwiązanie ze skanu.

Szkolniak: W takim razie wrzucam link do rozwiązania: https://imgur.com/a/f0vjqv2 Jak czegoś nie widać albo jakieś wątpliwości masz to pisz, bo aż jestem ciekaw co tam zepsułem

chichi: @Szkolniak sprawdź te wyniki w wolframie i zobacz co otrzymasz

Szkolniak: Hmm, wychodzi na to że pomysł był dobry i całki zapisałem też dobrze, tylko po prostu w którymś momencie je źle policzyłem Dzięki za wyłapanie błędu, potem jak przysiądę w wolnej chwili to postaram się znaleźć błąd

kerajs: Na skanie nie widzę błędu. Pozostaje wrzucić to w kalkulator (pamiętając o przestawieniu kąta na radiany) i wyliczyć przybliżoną wartość.

321:

Mariusz: Szkolniak no to sprawdźmy tę twoją całkę

1
	∫08/5 x dx +∫8/54 (4−√x(8−x))dx
2

∫_8/5⁴ (4−√x(8−x))dx √x(8−x)=xt x(8−x)=x²t² 8−x = xt² 8 = x+xt² 8=x(1+t²)

	8
x=
	1+t2

	8t
√x(8−x)=
	1+t2

	0*(1+t2)−8*2*t
dx =		dt
	(1+t2)2

	16t
dx = −		dt
	(1+t2)2

	√x(8−x)
t=
	x

	8		8   8   (8− ) 5   5
x =		, t2=
	5		64   25

	8		8   32   * 5   5
x =		, t2=
	5		64   25

	8
x =		, t2 = 4
	5

	4(8−4)
x = 4 , t2=
	42

x = 4 , t²=1

	8t		16t
∫21(4−		)(−		)dt
	(1+t2)		(1+t2)2

	8t		16t
∫12(4−		)		dt
	(1+t2)2		(1+t2)2

	64t		128t2
∫12		dt − ∫12		dt
	(1+t2)2		(1+t2)3

	32		32t(−4t)
=−		|12 + ∫12		dt
	1+t2		(1+t2)3

	32		32t		32
=−		+16+		−∫12∫		dt
	5		(1+t2)2		(1+t2)2

	48		64		32
=		+		−8−∫12∫		dt
	5		25		(1+t2)2

	104		32
=		−∫12∫		dt
	25		(1+t2)2

	104		32+32t2−32t2
=		−(∫12		dt)
	25		(1+t2)2

	104		32		32t2
=		−(∫12		dt−∫12		dt)
	25		1+t2		(1+t2)2

	104		32		16t(−2t)
=		−(∫12		dt+∫12		dt)
	25		1+t2		(1+t2)2

	104		32		16t		16
=		−(∫12		dt+		|12−∫		dt)
	25		1+t2		1+t2		1+t2

	104		16t		1
=		−(		|12 + 16∫12		dt)
	25		1+t2		1+t2

	104		32
=		−(		−8+16arctg(t)|12)
	25		5

	104		8
=		−(−		+16arctg(2)−4π)
	25		5

	144
=		+4π−16arctg(2)
	25

1
	∫08/5 x dx +∫8/54 (4−√x(8−x))dx=
2

x2		144
	|08/5 + (		+4π−16arctg(2))=
4		25

16		144
	+(		+4π−16arctg(2))=
25		25

160
	+4π−16arctg(2)=
25

32
	+4π−16arctg(2)
5

chichi: Wynik jest poprawny, ale odpuściłbym sobie ten sposób, można lepiej i duuuuużo szybciej

Mariusz: Wynik tej całki różni się od tego co otrzymał kerajs Nie sprawdzałem czy całka została przez Szkolniaka dobrze zapisana

chichi: @Mariusz ja nie sprawdzałem ani wyników @Szkolniak − tego nie chciało mi się sprawdzać, a @kerajs − tego upraszczać. Twój wynik jest tutaj końcu w czytelnej postaci i to o nim napisałem, że jest poprawny, jeżeli ich wyniki są różne, to są błędne

chichi: Różne od tego podanego przez Ciebie rzecz jasna

Mariusz: To że samą całkę oznaczoną dobrze policzyłem to wiem bo sprawdzałem ale nie sprawdzałem czy Szkolniak dobrze zapisał tę swoją całkę Na pierwszy rzut oka całka wygląda na dobrze zapisaną (Gdy liczyłem trzy całki oddzielnie to nie popełniłem błędu podczas obliczeń a gdy liczyłem tę całkę we wpisie z 12 wrz 2021 18:49 to popełniłem błąd i musiałem go szukać Znalazłem go jednak przed wysłaniem odpowiedzi) "można lepiej i duuuuużo szybciej" Nie wykluczone ale zobacz sam przyznałeś że wynik jest poprawny i przedstawiony w czytelny sposób w przeciwieństwie do wyników Szkolniaka i kerajsa Można trochę inaczej

1
	∫08/5 x dx +∫8/54 (4 − √x(8−x))dx=
2

1
	∫08/5 x dx+4∫8/54dx−∫8/54 √x(8−x)dx=
2

x2
	|08/5+4x|8/54−∫8/54 √8x−x2 dx
4

16		32
	+16−		−∫8/54 √8x−x2 dx
25		5

256
	− ∫8/54 √8x−x2 dx
25

	(x−4)(8−2x)
∫8/54 √8x−x2 dx = (x−4)√8x−x2|8/54−∫8/54		dx
	2√8x−x2

	(x−4)2
∫8/54 √8x−x2 dx = (x−4)√8x−x2|8/54+∫8/54		dx
	√8x−x2

	16−(x−4)2
∫8/54 √8x−x2 dx = (x−4)√8x−x2|8/54−∫8/54		dx
	√8x−x2

	1
+16∫8/54
	√16−(x−4)2dx

	1
2∫8/54 √8x−x2 dx =(x−4)√8x−x2|8/54+4∫8/54		dx
	√1−((x−4)/4)2

	x−4
2∫8/54 √8x−x2 dx = −(8/5−4)√64/5−64/25+16arcsin(		)|8/54
	4

	96		x−4
2∫8/54 √8x−x2 dx =		√4/25+16arcsin(		)|8/54
	5		4

	96		3
2∫8/54 √8x−x2 dx = 2*		+2*(8*0+8*arcsin(		))
	25		5

	96		3
∫8/54 √8x−x2 dx =		+8*arcsin(		)
	25		5

256		96		3
	− (		+8*arcsin(		))
25		25		5

	32		3
=		− 8arcsin(		)
	5		5

chichi:

	4
5k = 4 ⇒ k =
	5

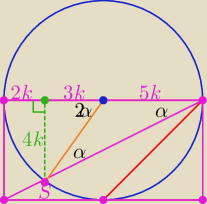
	1		42π		32		1
S = 10k2 + 42arctan(		) −		=		+ 16arctan(		) − 4π
	2		4		5		2

Tu potwierdzenie wyniku @Mariusz − szybko i sprytnie

Szkolniak: To już nie wiem co jest nie tak.. Sprawdzałem wasze wyniki z moim na wolframie, potem liczyłem kilka razy ponownie swoją całkę, sprawdzałem równości wyników (bo może były tylko w innej formie) I wyszło w końcu na to że gdzieś na pewno popełniam błąd w całce _8/5⁴∫√x(8−x)dx, bo tylko z tego mi wychodzi niepoprawna część w odpowiedzi

Mariusz: chichi no fajnie tylko jeśli zadanie to pojawiło się na analizie to mogliby tego nie uznać a jeśliby się nie pojawiło na analizie to mogliby chcieć dodatkowo komentarza do tego rysunku i do tej odpowiedzi Szkolniak jeśli chodzi o policzenie tej całki z pierwiastka to podstawienie którego użyłem to trzecie podstawienie Eulera Dalej możesz użyć metody Ostrogradskiego wydzielenia części wymiernej całki albo skorzystać z wzoru redukcyjnego Możesz też zrezygnować z podstawień i tę całkę liczyć przez części To że coś z twoim wynikiem było nie tak można było wywnioskować nie tyle że dostałeś ujemną wartość pola co ta wartość była większa od wartości pola tego "dolnego trójkąta" Wygląda na to że dobrze zapisałeś całkę a popełniłeś błąd podczas obliczeń więc nie zabraliby ci aż tak dużo punktów Szkolniak ty liczyłeś tę całkę modnym podstawieniem cyklometrycznym a nie sposobami które zaproponowałem Pokazałbyś dokładniejsze obliczenia tej całki ? Wtedy może wyłapałbym błąd Wynik kerajsa choć mieści się w dopuszczalnym przedziale to i tak intuicja podpowiada nam że jest on zbyt duży

chichi: @Mariusz wątpię.. To Wy rzuciliście je w układ i potraktowaliście całką, a nie autor zadania

Szkolniak: Mariusz ja się przyznam że początek pomysłu zaczerpnąłem z internetu, bo na ten moment nie mam aż takiej wiedzy w całkach aby samemu wpadać na takie podstawienia Liczyłem w ten sposób: ∫√x(8−x)dx=∫√−x²+8x−16+16dx= =∫√16−(x−4)²dx Podstawienie: x−4=u → dx=du ∫√16−(x−4)²dx= =∫√16−u²du Podstawienie: u=4sin(t) → du=4cos(t)dt ∫√16−u²du= =∫√16−16sin²(t)*4cos(t)dt =16∫|cos(t)|*cos(t)dt I tutaj się zastanawiałem, bo jeśli byłaby to całka nieoznaczona, to wypadałoby rozpatrzeć dwa przypadki, ale w naszym przykładzie mamy dany przedział, w którym funkcja f(t)=cos(t) jest ujemna, więc czy w takim razie możemy przyjąć że będzie tam minus?

Mariusz: Szkolniak sprawdź jeszcze czy aby na pewno powinieneś mieć te minusy w argumencie tych arcusów

chichi: Sprawdź sobie to na przykładzie jakiejś prostej całki z modułem np. ₄∫⁸ |x|dx = ₄∫⁸ xdx, bo dla x∊[4,8] f(x)=x, gdzie f(x)={x dla x≥0, −x dla x<0} ₋₂∫⁶ |x|dx = ₋₂∫⁰ (−x)dx + ₀∫⁶ xdx itd.

chichi: @Mariusz gdzie jakoś porządnie piszą o metodzie Ostrogradskiego?

Mariusz: Szkolniak sprawdź czy w twoim rozwiązaniu z 12 wrz 2021 18:49 aby na pewno powinieneś mieć minusy w argumencie tych arcusów sinusów Ty masz

	256		−3		−3
P =		−4sin(2arcsin(		))−8arcsin(		)
	25		5		5

ale czy aby na pewno te minusy w argumencie arcusów sinusów są potrzebne ? Wg mnie tu może być błąd

Mariusz: chichi ja o metodzie Ostrogradskiego czytałem u Fichtenholza w znanym trzytomowym podręczniku W paragrafie o wydzieleniu części wymiernej całki

Mariusz: No i mamy błąd opuszczając wartość bezwzględną nie zmieniłeś znaku

Szkolniak:

	3		x−4
No cały ten ułamek '−		' spowodowany jest tym że dostajemy postać arcsin(		), gdzie
	5		4

	8
za x podstawiamy ułamek		, czyli:
	5

8   −4 5		8		2		3
	=		−1=		−1=−
4		20		5		5

Dosyć chaotycznie, ale mam nadzieję że nie trzeba teraz aż tak wchodzić w szczegóły Co więc masz na myśli z tymi minusami?

chichi: @Mariusz też tam czytałem, miałem na myśli coś obszerniejszego, jutro poszperam w necie. P.S. W którym miejscu nie zmieniłem znaku?

Szkolniak: Okej spróbuję jeszcze raz, ale tym razem na forum.. Kontynuuję całkę: 16∫|cos(t)|*cos(t)dt= =−16∫cos²(t)dt= Zamieniamy cos²(t):

	1
cos(2t)=2cos2(t)−1 → cos2(t)=		(cos(2t)+1)
	2

Wracamy do całki: =−8∫(cos(2t)+1)dt= =−8∫cos(2t)dt−8∫dt= =−8sin(t)cos(t)−8t=−4sin(2t)−8t No i wracamy od 't' do 'x':

	u		u
u=4sin(t) → sin(t)=		→ t=arcsin(		)
	4		4

	x−4
u=x−4 → t=arcsin(		)
	4

	x−4		x−4
Zatem: ∫√x(8−x)dx=−4sin(2t)−8t=−4sin(2arcsin(		))−8arcsin(		)
	4		4

Po wbiciu do wolframa 'derivative of −4sin(2arcsin((x−4)/4))−8arcsin((x−4)/4)' w ''Alternate forms'' wyskakuje nasza postać Masakra, strasznie namieszane już z tym przykładem

Szkolniak: Dzięki za rozpisanie chichi i właśnie też mi się tak wydawało, bo to dosyć intuicyjne i chyba już kiedyś nawet robiłem przykład z takim modułem Tylko że to była całka oznaczona i wiedziałem że w danym przedziale nasza funkcja przyjmuje wartości ujemne, a tutaj obliczając całkę nieoznaczoną chyba trzeba rozpatrzeć dwa przypadki

Mariusz: chichi to Szkolniak nie zmienił znaku po opuszczeniu modułu podczas liczenia całki i dlatego otrzymał błędny wynik Jeśli chodzi o wydzielenie części wymiernej całki to Zakładasz że stopnie liczników są mniejsze niż stopnie odpowiadających im mianowników (tzw funkcje wymierne właściwe) Jeśli nie są to można wykonać dzielenie wielomianów oraz że mianownik posiada pierwiastki wielokrotne (nieważne czy rzeczywiste czy zespolone choć większą korzyść mamy gdy są zespolone bo dla rzeczywistych łatwiej ułamki proste scałkować) Jeśli ne mamy pierwiastków wielokrotnych to wydzielenie części wymiernej całki nic nam nie da i najczęściej będziemy musieli zastosować rozkład na sumę ułamków prostych chyba że zauważymy jakieś podstawienie Mamy całkę postaci

	L(x)
∫		dx , gdzie M(x) posiada pierwiastkl wielokrotne oraz deg M(x) > deg L(x)
	M(x)

Całka ta może być przedstawiona w sposób następujący

	L(x)		L1(x)		L2(x)
∫		dx=		+∫		dx
	M(x)		M1(x)		M2(x)

Na początku obliczamy mianowniki Jeżeli mamy dany rozkład mianowniki na czynniki to z niego korzystamy M₂(x) posiada te same pierwiastki co M(x) tyle że pojedyncze Czynniki mianownika M₁(x) dobieramy tak aby razem z czynnikami mianownika M₂(x) dawały rozkład mianownika M(x) na czynniki bo iloczyn wielomianów M₁(x) oraz M₂(x) ma być równy wielomianowi M(x) Tutaj aby to było trochę bardziej zrozumiałe przydałby się jakiś przykład Jeżeli nie mamy podanego rozkładu mianownika M(x) na czynniki to nie musimy tego mianownika M(x) rozkładać M₁(x) możemy wtedy policzyć licząc NWD(M(x),M'(x)) algorytmem Euklidesa czyli biorąc reszty z kolejnych dzieleń Mamy wtedy że M₁(x) = NWD(M(x),M'(x)) oraz M(x) = M₁(x)M₂(x) Jeżeli chodzi o liczniki to wiemy że stopnie liczników są mniejsze niż stopnie odpowiadających im mianowników ale jednak aby te liczniki wyznaczyć przyjmujemy współczynniki literowe za współczynniki tych wielomianów i różniczkujemy obustronnie równość

	L(x)		L1(x)		L2(x)
∫		dx=		+∫		dx
	M(x)		M1(x)		M2(x)

aby je obliczyć Podczas różniczkowania trzeba będzie skorzystać ze wzoru na pochodną ilorazu Ja współczynniki liczników indeksuję dzięki czemu nie ma obawy że mogą się nam literki w alfabecie skończyć Szkolniak arcus sinus jest funkcją nieparzystą więc mógłbyś się tego minusa pozbyć ale błąd powstał gdy nie zmieniłeś znaku po opuszczeniu modułu podczas liczenia swojej całki

Szkolniak: Z minusem jest źle.. Rozważmy wynik całki z dwoma znakami, tzn. z plusem oraz z minusem (stałą pomińmy).

	x−4		x−4
∫√x(8−x)dx=±(4arcsin(2arcsin(		))+8arcsin(		))
	4		4

Rozważmy teraz tą samą całkę, ale w przedziale, tzn.:

	x−4		x−4
8/54∫√x(8−x)dx=±[4arcsin(2arcsin(		))+8arcsin(		)]8/54
	4		4

Wprowadźmy oznaczenia:

	8   −4 5		8   −4 5
a=4arcsin(2arcsin(		)) oraz b=8arcsin(		)
	4		4

Po wstawieniu pod 'x' granic całki, dostajemy dwie opcje: _8/5⁴∫√x(8−x)dx=±((0−0)−(a+b))=±(0−(a+b))=±(−(a+b)) (1) jeśli mamy pierwotnie plus, otrzymujemy +(−(a+b))=−(a+b) (2) jeśli mamy pierwotnie minus, otrzymujemy −(−(a+b))=(a+b) Wrócmy teraz do tego ile wynosi pole P:

	256
P=		−8/54∫√x(8−x)dx=
	25

	256
=		−{±(−(a+b))}
	25

Odnieśmy się do rozpatrywanych (1) oraz (2): ad (1) pierwotnie plus (czyli nie tak, jak zakładaliśmy)

	256		256
P=		−(−(a+b))=		+(a+b)
	25		25

ad (2) pierwotnie minus

	256		256
P=		−((a+b))=		−a−b
	25		25

No i opcja druga wyszła taka jak mi tutaj, gdzie zmieniłem znak na minus po opuszczeniu modułu. Wychodzi więc na to że zmieniać znaku nie powinniśmy..

Szkolniak: to jakieś moje rozmyślania i burza mózgów, więc zagłębiać się w to Mariusz nie musisz − po prostu z tego rozumowania wychodzi na to że minusa tam nie powinno być, czyli opuszczamy moduł zostawiając plus. No i w ten sposób wynik wychodzi prawidłowy, sprawdziłem na wolframie i opcja pierwsza jest poprawną odpowiedzią Ale na dzisiaj starczy, bo już późno, także dobrej nocy

Mariusz: No to może przykład metody Ostrogradskiego wydzielenia części wymiernej całki

	64t3−128t2+64t
∫		dt
	(1+t2)3

Tutaj rozkład mianownika mamy podany więc M₂(t) = 1+t² // Te same czynniki co M(t) tyle że pojedyncze M₁(t) = (1+t²)² // razem mają dać rozkład mianownika M(x) na czynniki Wiemy że stopień licznilka L₁(t) jest równy co najwyżej trzy a stopień licznika L₂(t) jest równy co najwyżej jeden Za współczynniki liczników obieramy współczynniki literowe wstawiamy do równości

	L(t)		L1(t)		L2(t)
∫		dt =		+∫		dt
	M(t)		M1(t)		M2(t)

	64t3−128t2+64t		a3t3+a2t2+a1t+a0
∫		dt=
	(1+t2)3		(1+t2)2

	b1t+b0
+∫		dt
	1+t2

64t3−128t2+64t
	=
(1+t2)3

(3a3t2+2a2t+a1)(1+t2)2−4t(a3t3+a2t2+a1t+a0)(1+t2)
(1+t2)4

	b1t+b0
+
	1+t2

64t3−128t2+64t
	=
(1+t2)3

(3a3t2+2a2t+a1)(1+t2)−4(a3t4+a2t3+a1t2+a0t)
(1+t2)3

	b1t+b0
+
	1+t2

64t³−128t²+64t=(3a₃t²+2a₂t+a₁)(1+t²)−4(a₃t⁴+a₂t³+a₁t²+a₀t) +(b₁t+b₀)(1+t²)² 64t³−128t²+64t=3a₃t²+2a₂t+a₁+3a₃t⁴+2a₂t³+a₁t² −4a₃t⁴−4a₂t³−4a₁t²−4a₀t+b₁t⁵+2b₁t³+b₁t+b₀t⁴+2b₀t²+b₀ 64t³−128t²+64t=b₁t⁵+(b₀−a₃)t⁴+(2b₁−2a₂)t³ +(2b₀+3a₃−3a₁)t²+(b₁+2a₂−4a₀)t+a₁+b₀ b₁=0 b₀−a₃=0 2b₁−2a₂=64 2b₀+3a₃−3a₁=−128 b₁+2a₂−4a₀=64 a₁+b₀=0 b₁=0 b₀=a₃ a₁=−a₃ a₂=−32 a₃=−16 a₀=−32

	64t3−128t2+64t		−16t3−32t2+16t−32		1
∫		dt =		−16∫		dt
	(1+t2)3		(1+t2)2		1+t2

	64t3−128t2+64t		−16t3−32t2+16t−32
∫		dt =		−16arctg(t)+C
	(1+t2)3		(1+t2)2

Mariusz: Szkolniak , tak czy inaczej w twoim rozwiązaniu z 12 wrz 2021 18:49 jest problem z minusami Ze względu na nieparzystość sinusa oraz arcus sinusa nie jest ważne gdzie zmienisz znak aby ten wynik poprawić (jak zmienisz znaki przed tymi dwoma składnikami gdzie masz sinus i arcus sinus wynik będzie dobry, jak zmienisz znaki w argumencie arcus sinusa też będzie dobrze)

kerajs: ''Mariusz: Nie wykluczone ale zobacz sam przyznałeś że wynik jest poprawny i przedstawiony w czytelny sposób w przeciwieństwie do wyników Szkolniaka i kerajsa'' Co za bajki opowiadasz? Wynik który podałem jest i poprawny, i czytelnie przedstawiony. PS Edytory nie rozróżniają kontekstów i czasem błędnie odrzucają poprawną pisownię. Tu ma być ''niewykluczone'' zamiast '' nie wykluczone''.

Mariusz: Czepiasz się Ta poprawny , taki mały skrawek a ponad połowę pola trójkąta by miał, Tylko jakoś dziwne że zarówno chichiemu jak i Szkolniakowi inne wyniki wyszły Gdzieś się pomyliłeś i nie chcesz się do tego przyznać

Mariusz: No tak teraz dopiero zauważyłem że masz tam arcusa cotangensa i jak tak to jest poprawny choć tu chichi ma rację że nie jest on czytelny

chichi: @Mariusz dlatego lepiej używać tan i cot zamiast tg i ctg, bo później takie pomyłki wychodzą. Nie wiem czemu miało służyć to spolszczenie, może Ty wiesz?

Mila: Wynik mam jak u chichi z dokładnością do 3 miejsca po przecinku . Korzystałam z arcsin−sa.

Szkolniak: Ja już tyle razy te zadanie liczyłem że chyba sobie odpuszczę − przyjmę że wystarczy skorzystać z tego że funkcja jest nieparzysta, wyciągnąć minus z argumentu przed i wtedy wynik wychodzi okej Też chichi mówiłeś że to my osadzilismy te zadanie w układzie współrzędnych i to prawda Ogólnie takie zadanie to i tak ponad mój poziom więc byłem ciekaw czy jestem w stanie w ten sposób je zrobić, bo tylko taki pomysł wpadł mi do głowy

chichi: @Szkolniak słuchaj I tak szacun, że się podjąłeś, co więcej pomysł był poprawny tylko umiejętności nie pozwoliły, aby to poprawnie dociągnąć do końca. Niech żałuje ten co nie robi nic, Ty możesz być jedynie dumny z samego siebie

Szkolniak: To prawda, ogólnie jestem zdania że taka samodzielna nauka matematyki w domu jest bardzo dobra i dużo daje, bo gdyby się miało polegać tylko na wiedzy szkolnej i na takim poziomie nauczania, to byłoby moim zdaniem bardzo ciężko

chichi: Według mnie najlepszymi matematyki są samoucy, gdy sam przez wszystko przechodzisz, rozumiesz mechanizmy i działanie co, jak i dlaczego, a nie schematy zaczerpnięte od nauczycieli czy prowadzących, choć Ci również wielką rolę w tej drodze nauczania odgrywają. Matematyka to też styl życia, czego dobrym przykładem jest właśnie to forum i stali jego bywalcy P. S. W szkole nie nauczają matematyki, tylko umiejętności rozwiązywania zadań, a to tylko część tej cudownej dziedziny i od razu zaznaczam, że to moje subiektywne zdanie

kerajs: ''chichi: @Mariusz dlatego lepiej używać tan i cot zamiast tg i ctg, bo później takie pomyłki wychodzą. Nie wiem czemu miało służyć to spolszczenie, może Ty wiesz? '' To polskojęzyczne forum, więc użycie oznaczeń ogólnie znanych (bo uczonych w polskich szkołach) nie powinno dziwić. A arkusa kotangensa wybrałem dlatego, że tylko on ma całkowity argument, więc i najkrótszy zapis w tutejszym edytorze. ''Mariusz: choć tu chichi ma rację że nie jest on czytelny'' Chichi nic takiego nie napisał. Bez urazy, ale może źle widzisz i czas na okulary?

Szkolniak: Schematy też są dobre, bo jednak jeśli je stosujesz i są one odpowiednie to mogą wyrabiać dobre nawyki, pod warunkiem że rozumie się każdy krok i rozumowanie, tzn. co się z czego bierze itd. Według mnie w szkole jest też trochę mało nauczania pod względem takiego zwyczajnego analizowania zadania, mam na myśli że czytając zadanie powinien się nasuwać na myśl jakiś pomysł na rozwiązanie, a nie że nie wiesz od czego zacząć pierwszą linijkę Kiedyś patrzyłem na zadania z IMO, to chyba właśnie tam nawet tacy młodsi po 15 lat robili takie zadania, że nie mam pytań..

chichi: @kerajs ja nie mam do Ciebie pretensji, że ich użyłeś, bo wiem, że takowych się używa w polskim systemie nauczania, moje pytanie było dlaczego akurat takich I w jakim celu zmienione te, których używa reszta świata, bo ja widzę tylko minusy, jednym z nich właśnie takie pomyłki

Mariusz: Karajs no fajnie skoro twój wynik jest taki czytelny to dlaczego akurat chichi wybrał do porównania wynik całki którą ja policzyłem poza tym podany przez ciebie wynik nie jest uproszczony " A arkusa kotangensa wybrałem dlatego, że tylko on ma całkowity argument, więc i najkrótszy zapis w tutejszym edytorze. " To akurat nie jest prawda vide mój wynik całki Szkolniaka policzonej trzecim podstawieniem Eulera za to trzeba się dobrze wczytywać w ten wynik bo łatwo go pomylić z arcusem tangensem

Mariusz: W tym ostatnim zdaniu chodziło mi o to że trzeba się dobrze wczytywać w ten wynik przedstawiony przez kerajsa bo łatwo go pomylić z arcusem tangensem ale już trichę zmęczony jestem i jeszcze ten brak edycji

kerajs: ''chichi: wiem, że takowych się używa w polskim systemie nauczania, moje pytanie było dlaczego akurat takich I w jakim celu zmienione te, których używa reszta świata, bo ja widzę tylko minusy, jednym z nich właśnie takie pomyłki'' Tak naprawdę to jest to pytanie dla historyka matematyki. Ja nim nie jestem, ale mam pewną hipotezę. Sądzę że było odwrotnie. Przed II WŚ głównym językiem matematyki był język francuski. Funkcje trygonometryczne używane wtedy we Francji miały oznaczenia: sin , cos , tg, cotg. Po wojnie anglosasi (głównie USA) zdominowali naukowy zachód wprowadzając swoje oznaczenia, Jednak za żelazną kurtyną francuski nadal był ważniejszy od angielskiego i stąd pozostanie przy ww oznaczeniach. W niektórych krajach w formie niezmienionej (np: Czechy, Słowacja), lub z drobnymi zmianami np: ctg zamiast cotg ( Polska, Rosja)

chichi: @kerajs dzięki za to, brzmi przekonująco, aczkolwiek moje podejście do zapisów, które preferuje jest następujące: sinus od 3 pierwszych liter − sin, cosinus (cofunction) − cos, tangens od 3 pierwszych liter − tan, cotangens (cofunction) − cot P. S. Poznałem wielu matematyków z krajów, w których mówią po hiszpańsku i na sin(x) piszą sen(x)

kerajs: Kolejne hipotezy: 1. Pewnie dlatego tak robią, że w hiszpańskim ''sin'' jest słowem potocznym. 2. Możliwe, że w łacinie słowa ''tan'' i ''cot'' także miały ustalone znaczenie, więc przyjęto mniej oczywiste skróty. Sądzę, że zapis powinien być zrozumiały dla odbiorców i dlatego, niezależnie od preferencji, na anglojęzycznym forum pisałbym 'cot', na polskojęzycznym 'ctg', a 'cotg' na forum czeskim