Implikacja, czworokąty
Ula: Oceń czy ta implikacja jest prawdziwa:
,,Jeśli czworokąt ma dwie przekątne równej długości, to ten czworokąt jest trapezem
równoramiennym."
Uważam, że ta implikacja jest prawdziwa. Tylko teraz zastanawiam się czy prostokąt i kwadrat są
trapezami równoramiennymi? Mają co najmniej jedną parę boków równoległych, co najmniej dwa
boki równej długości oraz równe kąty przy podstawie (wszystkie cechy, które musi spełniać
trapez równoramienny), więc wydaje mi się że tak.
Z góry bardzo dziękuję

10 wrz 14:35
mat: tak

10 wrz 15:15
Ula: Chyba jednak obali tą implikację deltoid.
10 wrz 15:21
mat: a no masz racje!
10 wrz 15:23
Ula: A może da się znaleźć jeszcze jakiś inny przykład 🤔
10 wrz 15:24
mat:
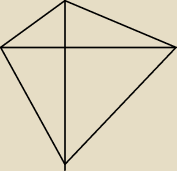
10 wrz 15:26
Ula: Pewnie jeszcze dowolny czworokąt, który nie jest trapezem
10 wrz 15:29
Ula: Czyli:
1) jedynymi przykładami, które obalą tę implikację mogą być: czworokąt, który nie jest trapezem
oraz deltoid?
2) kwadrat i prostokąt są trapezami równoramiennymi
3) równoległobok nie jest trapezem równoramiennym
Z góry bardzo dziękuję czy każdy punkt napisałam poprawnie

10 wrz 15:39
mat: równoległobok jak najbardziej jest trapezem równoramiennym
10 wrz 15:40
mat: 1) deltoid tez jest czworokątem niebędącym trapezem (w ogólności)
10 wrz 15:41
ite:
Żeby ta implikacja była zawsze prawdziwa, potrzebny jest jeszcze jeden warunek: punkt
przecięcia musi dzielić te równe przekątne w takich samych proporcjach (np. na obu 1:5).
Czworokąty niespełniające tego warunku a mające równe przekątne, możesz podawać jako dowód
fałszywości tej implikacji (dają prawdziwy poprzednik i fałszywy następnik).
10 wrz 15:48
ite: Czy to jest znowu z tego podręcznika do 8 klasy? Jeśli nie, to jakiego poziomu nauczania jest
to zadanie?
Pytam, bo odpowiedzi z 15:39 nie są prawidłowe, ale nie mam pojęcia, jakie własności implikacji
poznaje uczeń podstawówki.
10 wrz 16:31
Ula: to zadanie z pierwszej klasy szkoły średniej z poziomu podstawowego
10 wrz 17:50
ite: OK, szkoła średnia.
Mamy podane twierdzenie w formie implikacji:
Jeśli czworokąt ma dwie przekątne równej długości (założenie), to ten czworokąt jest
trapezem równoramiennym (teza).
Teraz można udowodnić to twierdzenie (i mieć pewność, że jest prawdziwe) lub podać
kontrprzykład czyli przykład czworokąta, dla którego implikacja będzie fałszywa (i mieć
pewność, że twierdzenie nie jest prawdziwe).
Jak podać właściwy kontrprzykład?
Implikacja będzie fałszywa tylko wtedy gdy poprzednik (tutaj to założenie) jest prawdziwy
a następnik fałszywy (teza). Czyli trzeba znaleźć taki czworokąt, który ma równe
przekątne ale nie jest trapezem równoramiennym.
Wracamy do 15:39
3) równoległobok nie jest trapezem równoramiennym ← to nie jest właściwy kontrprzykład
każdy równoległobok spełnia tezę ( jest trapezem równoramiennym), nie każdy spełnia założenie
(nie każdy równoległobok ma przekątne równej długości),
2) kwadrat i prostokąt są trapezami równoramiennymi ← to również nie jest właściwy
kontrprzykład
oba spełniają warunki zarówno podane w tezie jak i w założeniu
1) jedynymi przykładami, które obalą tę implikację mogą być: czworokąt, który nie jest trapezem
oraz deltoid
czworokąt, który nie jest trapezem, może nie mieć równych przekątnych ← nie ma gwarancji że
spełnia założenie, za mało warunków.
Ale jednym z takich czworokątów jest deltoid. Trzeba wybrać taki, który ma równe przekątne i
nie ma wszystkich boków równych. Mamy spełnione założenie i nie spełnioną tezę, czyli podana
implikacja jest fałszywa.
11 wrz 09:33
Eta:
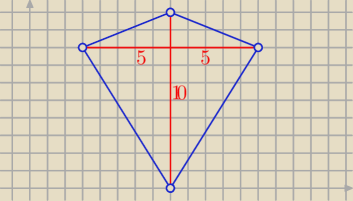
kontrprzykład
Zatem : taka implikacja jest fałszywa
11 wrz 10:52




 kontrprzykład
Zatem : taka implikacja jest fałszywa
kontrprzykład
Zatem : taka implikacja jest fałszywa