trygonometria ~dudu: cos4x+scos2x=0 2cos3xcosx=0 cos3x=0 ⋁ cosx=0

	π
3x=		+ 2kπ (potem podzielić na 3) ale nie rozumiem okresu bo powinno być kπ dlaczego ?
	2

	π
i w drugim x=		+ 2kπ a powinno być kπ dlaczego narysowałem cos 3x owszem będzie ciasny
	2

wykres, ale w cos x będzie normalny, wytłumaczcie gubię się w okresach

chichi: To spójrz na wykres cosinusa, co jaki czas pojawiają się miejsca zerowe?

~dudu:

π
	ale to jest wykres 3x
2

chichi: Jak się gubisz to stosuj podstawienie:

	π		π
3x=t i wtedy masz cos(t)=0 ⇔ t=		+kπ ⇔ 3x=		+kπ
	2		2

chichi:

	π
No to źle patrzysz, jesli widzisz, że co
	2

~dudu:

	π
okres cosx to T=2π miejsca zerowe		+kπ
	2

nie , nie chcę podstawienia chce zrozumiec, poczekam może ktos inny lepiej mi wytlumaczy zamiast cwaniakowac

mat:

	2π
1) Funkcja y=cos(3x) ma okres T=
	3

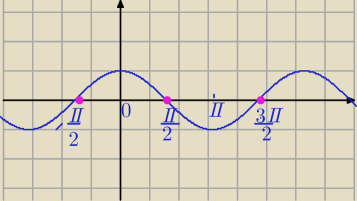
2) Rozwiązując równanie: cos(3x)=0 korzystamy z tego, że cosinus przyjmuje wartość 0 dla argumentów jak na rysunku, czyli

	π		3π		5π		7π
3x∊{....,		,		,		,		,.... } piszę tylko argumenty dodatnie,
	2		2		2		2

aby łatwiej było zrozumieć, zatem:

	π
3x=		+kπ, gdzie k∊C to jest dla potrójnego argumentu x
	2

	π		kπ
x=		+
	6		3

To podobny problem jak dla innych funkcji. Np. y=log₃(x) D=(0,∞) Równanie: 1) log₃(x)=0⇔ x=1 2) log₃(x−5)=0 x−5>0⇔x>5 D=(5,∞) (x−5)=1⇔ x=6 3) log₃(3x)=0 x>0 3x=1

	1
x=
	3

mat:

~dudu: Dziękuję bardzo teraz jaśniej i lepiej