 Uwaga
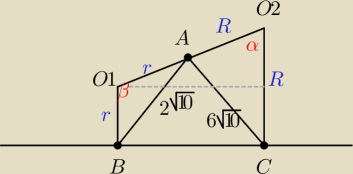
Uwaga  Rysunek nie jest w skali
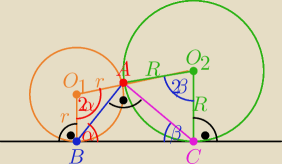
β = 180 − α
czyli cosβ = −cosα
stąd wiemy, że (tw. cosinusów):
40 = 2r2 + 2r2cosα −−> 20 = r2(1+cosα)
60 = 2R2 − 2R2cosα −−−> 30 = R2(1−cosα)
Rysunek nie jest w skali
β = 180 − α
czyli cosβ = −cosα
stąd wiemy, że (tw. cosinusów):
40 = 2r2 + 2r2cosα −−> 20 = r2(1+cosα)
60 = 2R2 − 2R2cosα −−−> 30 = R2(1−cosα)
| R−r | ||
dodatkowo: cosα = | ||
| R+r |
| R−r | R−r | |||
3r2( 1+ | ) = 2R2( 1 − | ) | ||
| R+r | R+r |
| 2R | 2r | |||
3r2 | = 2R2 | |||
| R+r | R+r |
| 3 | ||
3r = 2R −−−>R = | r | |
| 2 |
| 2R | 3r | 100 | ||||
20 = r2* | = r2 | −−−> r2 = | ||||
| R+r | 5r/2 | 6 |
| 25 | 1 | |||
|BC|2 = (r+R)2 − (R−r)2 = | r2 − | r2 = 6r2 = 100 −−> |BC| = 10 | ||
| 4 | 4 |
 ΔABC prostokątny |∡BAC|=90o
to BC2=(2√10)2+(6√10)2
|BC|=20
i po ptokach
ΔABC prostokątny |∡BAC|=90o
to BC2=(2√10)2+(6√10)2
|BC|=20
i po ptokach  @ wredulus (6√10)2 =360 ≠ 60
@ wredulus (6√10)2 =360 ≠ 60 