dowod beduin: Zadanie 8. (0−3) PAZDRO − matura rozszerzona Dany jest trójkąt prostokątny, którego jeden z kątów ostrych ma miarę 75°, a przeciwprostokątna

	1
ma długość c. Wykaż, że pole tego trójkąta jest równe S=		c2.
	8

mam taki pomysł aby zrobić, żę

	√2		√3		√2		1
sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°=		*		+		*		=
	2		2		2		2

	√6+√2
=		i teraz tak samo dla cosinusa i uzależnić od boków sinusa i cosinusa?
	4

chichi:

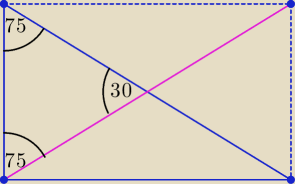
	1		1		1
S =		[		*c2*sin(30o)] =		c2 □
	2		2		8

P.S. Niech się Pazdro nie ośmiesza takimi dowodami, jaki to jest arkusz?

chichi: Twoim sposobem też wyjdzie, ale po co sobie życie utrudniać?

beduin: Nie wpadłem na to. Spróbuję dokończyć tym moim. Dzięki Matura próbna rozszerzona Pazdro marzec 2021r.

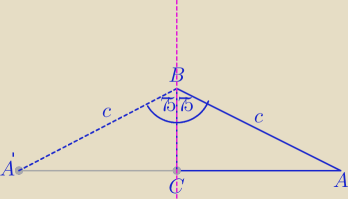
Mila: 1) ΔA'CB symetryczny do ACB względem prostej BC 2)

	1
2S=		c2*sin(150o)
	2

	1
2S=		c2*sin(30o)
	2

	1
2S=		c2
	4

	1
S=		c2
	8

========