Oblicz pole powierzchni Damian#UDM: Oblicz pole tej części powierzchni z=2y²−2x²+3xy , która spełnia nierówności: x²+y²≤1 , y≥x i y≥−x. Czy w tym zadaniu chodzi o: 1. Narysowanie obszaru, 2. Wyznaczenie obszaru całkowania, 3. Wyznaczenie granic całkowania, 4. Współrzędne biegunowe + Jakobian, 5. Obliczenie całki podwójnej?

mat: no to wiesz wszstko! Jak wyuglada obszar

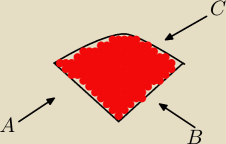
Damian#UDM: 1. Obszar A: y≥−x B: y≥x C: x²+y²≤9 S=(0,0), r=3 2. Parametryzacja 0≤r≤3 ^π₄≤α≤^3π₄ 3. Współrzędne biegunowe

⎧	x=r*cos(α)
⎨	y=r*sin(α)
⎩	J|r,α|=r

∫_D∫zdxdy=∫_^π4^3π₄∫₀³[2r²sin²(α)−2r²cos²(α)+3r²sin(α)cos(α)]drdα No i dalej już wystarczy policzyć

jc: W poleceniu jest mowa o polu. Liczysz więc całkę ∫∫ [1 +(dz/dx)² + (dz/dy)²)^1/2 dx dy =∫ ∫ (1+ 25(x²+y²) )^1/2 dx dy

	π
=		∫01 (1+ 25r2)1/2 r dr
	2

	π		1
=				[(1+25r2)3/2]01
	2		75

Damian#UDM: Ok, czyli jest na to wzór. Dziękuję za uwagę