trójkat 123: Wewnątrz trójkąta równobocznego o boku długości a wybrano punkt M. Wykaż,że suma odległości punktu M od wierzchołków trójkata jest nie większa niż 2a

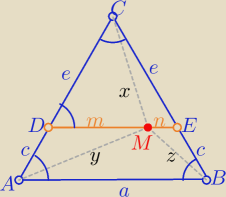
Eta: Teza: x+y+z≤ 2a c+e=a W równobocznym ΔCED : x<e i m+n=e z nierówności trójkąta ( w ADM i BEM y≤c+m z≤c+n i x<e +−−−−−− x+y+z<c+c+m+n+e= c+c+e+e= 2a równość zachodzi gdy punkt M pokrywa się z wierzchołkiem ΔABC zatem x+y+z≤2a c.n.w.

Eta: