Procenty Karolina: Oto ankieta którą przeprowadzono wśród dzieci oraz wyniki otrzymane przez ankieterów. Umie jeździć na nartach − 65% Nie umie jeździć na rowerze i na nartach − 0% Umie grać na instrumencie − 30% Umie śpiewać − 40% Nie umie grać ani śpiewać− 50% Umie jeździć rowerem − 100% Ile procent ankietowanych: a)potrafi jeździć na rowerze i na nartach b)potrafi jeździć na rowerze i nie potrafi grać na instrumencie c)potrafi grać i śpiewać d)potrafi grać i nie potrafi śpiewać. Poniżej wklejam skan tej treści zadania wraz z wykresami: https://pl-static.z-dn.net/files/dfe/490f37d575e55ecc7fdb5ae7214ed705.jpeg Napiszę swoje przemyślenia: a)100%+65%=165% 165%−100%=65% − potrafi jeździć na rowerze i na nartach c)30%+40%+50%=120% 120%−100%=20% − potrafi grać i śpiewać b)Skoro wszyscy potrafią jeździć na rowerze (100%), to po odjęciu procenta wszystkich osób, które potrafią grać (30%) mamy osoby, które potrafią jeździć na rowerze, ale nie potrafią grać (70%) d) w tym podpunkcie mam największy dylemat. 30%(sami grający oraz grający i śpiewający jednocześnie)−20%(grający i śpiewający jednocześnie)=10%(sami grający) Czy takie rozumowanie jest poprawne? W internecie znalazłam inne wyjaśnienie podpunktu d): (natomiast według mnie poprawne jest tylko moje powyższe wyjaśnienie) Wyjaśnienie z internetu: 40% −30%=10% Z góry bardzo dziękuję za odpowiedź

ite: Warto stosować diagramy do takich zadań.

Karolina: Rozumiem, ale diagramy spełnią swoją rolę tylko w podpunktach: a) i c) prawda? Ja głównie chciałam zapytać czy moje rozumowanie w podpunkcie d) jest poprawne? d) 30%(sami grający oraz grający i śpiewający jednocześnie)−20%(grający i śpiewający jednocześnie)=10%(sami grający) Osobiście wydaje mi się, że tak, natomiast w internecie znalazłam inne wyjaśnienie podpunktu d), które w ogóle mnie nie przekonuje, a oto one: 40% −30%=10% Jeszcze raz z góry bardzo dziękuję za odpowiedź

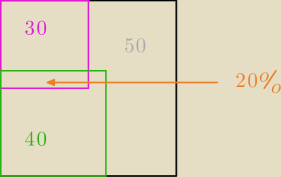
ite: W c/ raczej wnioskowanie: 100%−50%=50% (wszyscy minus ani nieśpiewający ani niegrający). Czyli grających lub śpiewających jest 50%, więc 30%+40%−50%=20% to część wspólna obu grup

Karolina: A czy w takim razie w c) moje rozumowanie jest błędne?

ite: d/ Wyjaśnienie z 16:00 30%(sami grający oraz grający i śpiewający jednocześnie)−20%(grający i śpiewający jednocześnie)=10%(sami grający) moim zdaniem jak najbardziej prawidłowe. Dla tego z internetu nie widzę uzasadnienia, a jak autor takiego wpisu je tłumaczył? c/ Napisałaś 30%+40%+50%=120%, dalej zauważasz, że skoro suma ma wynosić 100%, to 20% będzie częścią wspólną grup. I teraz pytanie których? Zsumowałaś dane dotyczące trzech grup, więc to może być część wspólna wszystkich trzech lub którejś z ich par. Z treści widzimy, że grupa szara jest rozłączna a różową i rozłączna z zieloną, ale gdyby tak nie było, to można by popełnić błąd.

Karolina: Rozumiem, czyli w tym zadaniu w podpunkcie c) moje rozumowanie również jest poprawne, natomiast w zadaniu o innej treści mogłoby już takie nie być. Jeszcze raz bardzo dziękuję