Grześ:
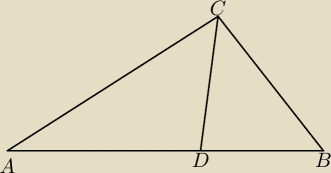
Wiedzac ze AC=x+y+z, DB=z, CD=x, CB=y oraz ∡DCB=40, ∡BDC=80 i ∡CBD=60 wyznacz ∡BAC.
27 sie 18:23
Mariusz:
∡BDC = 80
∡CDA = 100
| x+y+z | | x | |
| = |
| |
| sin(100) | | sin(∡DAC) | |
| sin(∡DAC) | | sin(100) | |
| = |
| |
| x | | x+y+z | |
| | x sin(80) | |
sin(∡DAC)= |
| |
| | x+y+z | |
| | x sin(80) | |
∡BAC=∡DAC = arcsin( |
| ) |
| | x+y+z | |
27 sie 21:04
Mariusz:
Trzeba obliczyć konkretne wartości dla x , y , z ?
Jeśli tak to zadanie nie jest jeszcze skończone
27 sie 21:08
chichi:
|∡BAC| = 20
o 
27 sie 21:10
chichi:
Mimo iż rysunek nie oddaje, spróbuję znaleźć drugie rozwiązanie, żeby potwierdzić ten wynik, no
chyba, że ktoś jeszcze otrzymał taki wynik @Mila @Eta @wredulus−pospolitus
macie jakieś propozycje?
27 sie 21:17
Mila:
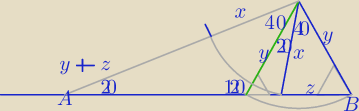
?
27 sie 21:38
Mariusz:
Z twierdzenia sinusów w DBC
| | 2√3 | | 2√3 | |
x+y+z=x(1+ |
| sin(80)+ |
| sin(40)) |
| | 3 | | 3 | |
3(x+y+z)=x(3+2
√3 sin(80) + 2
√3 sin(40))
| 3x | | 3 | |
| = |
| |
| 3(x+y+z) | | 3+2√3 sin(80) + 2√3 sin(40) | |
| | 3sin(80) | |
∡BAC = arcsin( |
| ) |
| | 3+2√3 sin(80) + 2√3 sin(40) | |
Mnie tyle wyszło po zabawie z trygonometrią
Da się to uprościć do 20° ?
27 sie 22:08
chichi:
Mam 2 rozwiązanie, które potwierdza, że |∡BCA| = 20
o, ale jestem na imprezie i piszę z
telefonu, jutro wstawie rozwiązania, bo na telefonie słabo się rysuje

27 sie 22:21
chichi:
|∡BAC| = 20o **
27 sie 22:25
Mariusz:
chichi no ok ,widać że to literówka tym bardziej że w poprzednim wpisie
poprawnie napisałeś jaki kąt obliczyłeś
Gdy wstawiłem swój wynik który otrzymałem z trygonometrii do kalkulatora
to też otrzymałem 20° tyle że aby to pokazać trzeba się trochę pobawić
i uprościć ułamek
| 3sin(80°) | |
| |
| 3+2√3sin(80°)+2√3sin(40°) | |
27 sie 22:56
Mariusz:
| 3sin(80°) | |
| |
| 3+2√3sin(80°)+2√3sin(40°) | |
| | 3 | |
=2sin(80°)cos(80°) |
| |
| | 6cos(80°)+2√3 2sin(80°)cos(80°)+4√3sin(40°)cos(80°) | |
| | 3 | |
=sin(160°) |
| |
| | 6cos(80°)+2√3sin(160°)+2√3 2sin(40°)cos(80°) | |
| | 3 | |
=sin(20°) |
| |
| | 6cos(80°)+2√3sin(20°)+4√3 sin(40°)cos(80°) | |
| | 3 | |
=sin(20°) |
| |
| | | | √3 | | 6cos(80°)+2√3sin(20°)+2√3( |
| − sin(40°)) | | | 2 | |
| |
| | 3 | |
=sin(20°) |
| |
| | | | √3 | | 6cos(80°)+2√3sin(20°)+2√3( |
| − sin(40°)) | | | 2 | |
| |
| | 3 | |
=sin(20°) |
| |
| | 3+6cos(80°)+2√3sin(20°)−2√3sin(40°) | |
| | 3 | |
=sin(20°) |
| |
| | | | 1 | | √3 | | 3+6(− |
| cos(40°)+ |
| sin(40°))+2√3sin(20°)−2√3sin(40°) | | | 2 | | 2 | |
| |
| | 3 | |
=sin(20°) |
| |
| | 3−3cos(40°)+√3sin(40°)+2√3sin(20°) | |
| | 3 | |
=sin(20°) |
| |
| | | | 1 | | √3 | | 3+2√3(sin(40°) |
| −cos(40°) |
| )+2√3sin(20°) | | | 2 | | 2 | |
| |
| | 3 | |
=sin(20°) |
| |
| | 3+2√3sin(40°− 60°)+2√3sin(20°) | |
| | 3 | |
=sin(20°) |
| |
| | 3+2√3sin(−20°)+2√3sin(20°) | |
| | 3 | |
=sin(20°) |
| |
| | 3−2√3sin(20°)+2√3sin(20°) | |
=sin(20°)
Czyli udało się uprościć wynik uzyskany sposobem trygonometrycznym
28 sie 00:02
chichi:
@
Mariusz dużo jeszcze nie wypiłem, ale jak to czytam to aż kręci mi się głowie

28 sie 00:16
Mariusz:
chichi coś nie lubisz trygonometrii co
W rozwiązaniu trygonometrycznym wykorzystałem to
że jeden z kątów w trójkącie CAD jest przyległy do kąta w trójkącie BDC o danej mierze
i następnie z twierdzenia sinusów
(raz w trójkącie CAD aby uzależnić wartość sinusa kąta ∡DAC od długości boków x,y,z
i dwa razy w BDC aby uzależnić długości boków y oraz z od x)
Po wstawieniu x oraz y i z uzależnionych od x do
| | x sin(80)° | |
sin(∡DAC) = |
| |
| | x+y+z | |
x się skrócił a dalej to tylko upraszczanie uzyskanego ułamka z czym też trochę zabawy było
28 sie 00:34
chichi:
@
Mariusz jak już wspominałem jestem zwolennikiem
geometrii syntetycznej co zresztą
widać po moich rozwiązaniach. Ty wszędzie jeden schemat, wciskasz trygonometrie bez
opamiętania i szczerze to zero w tym geometrii, tylko żmudne dłubanie w równaniu, czyli
algebra nie geometria. Wpaść na takie rozwiązania jakie prezentuje nie jest łatwo, ale I'm
problem trudniejszy tym lepszy. Czyż nie to właśnie jest pięknem
matematyki?

P. S.
Jutro wstawię oba rozwiązania i odpowiem na Twoje pytanie w poprzednim wątku, dobranoc
28 sie 05:23
kerajs:
''chichi: Ty wszędzie jeden schemat, wciskasz trygonometrie bez
opamiętania i szczerze to zero w tym geometrii, tylko żmudne dłubanie w równaniu, czyli
algebra nie geometria.''
To wynik narzędzi w jakie wyposaża uczniów system szkolnictwa. Szkoła skupia się na
analitycznych rozwiązaniach, stąd trygonometria czy tw. sinusów i kosinusów.
Sztuka geometrii jest uprawiana przez samouków, i to tych którym ktoś podsunie odpowiednie
książki.
PS
Podobnie jest ze sztuką rozwiązywania nierówności.
28 sie 19:47
chichi:
@
kerajs fakt, jestem samoukiem

28 sie 20:45
Mariusz:
Tutaj kerajs ma trochę racji
Czy trygonometria jest algebrą ?
Jaką masz definicję funkcyj trygonometrycznych ?
Jak wyprowadzasz wzory na sumę / różnicę funkcyj trygonometrycznych
czy na funkcje trygonometryczne sumy i różnicy
W jaki sposób udowadniasz tw sinusów i cosinusów
Gdybyśmy chcieli to zadanie Grzesia rozwiązywać szkolnymi sposobami
to twierdzenie sinusów tutaj można zastosować
W poprzednim zadaniu Grzesia zastosowanie miało tw cosinusów
choć twój pomysł z trójkątami przystającymi też był ok
jeśli chodzi o szkolne narzędzia jak to kerajs ujął
"Wpaść na takie rozwiązania jakie prezentuje nie jest łatwo"
No właśnie w tym problem a ludzie którzy wrzucają tu zadania
nie zawsze będą w stanie z samego rysunku odczytać sposobu rozwiązania
Jednak twoje rozwiązania gdy są zaprezentowane w zrozumiały sposób mogą się podobać
28 sie 21:20
Mariusz:
Kerajs miałeś jeszcze w szkole geometrię sferyczną ?
W geometrii sferycznej są odpowiedniki twierdzenia sinusów i cosinusów
ale suma miar kątów w trójkącie nie zawsze jest równa 180°
Geometria sferyczna może być przydatna np do pomiarów Ziemi i powinni ją zostawić
w programie nauczania
28 sie 22:26
chichi:
@
Mariusz
'żmudne dłubanie w równaniu, czyli algebra' czyli te przekształcenia równania etc. nie tryg.

28 sie 22:49
kerajs: Nie, nie miałem.
Przypuszczam że nikt (może prócz szkół średnich o profilu morskim, lotniczym albo geodezyjnym
?) geometrii nieeukidesowych nie miał w programie.
PS
Ziemię trochę trudno mierzyć, więc mało przydatna to umiejętność, moim zdaniem.
@chichi
Może zdradzisz od jakich książek zacząłeś samonaukę geometrii ?
28 sie 22:52
chichi:
@
kerajs od jakiego mniej więcej poziomu Ci chodzi?

30 sie 14:19
kerajs: Od poziomu 0 (przyjmując iż wiedza szkolna to −1).
31 sie 19:32
chichi:
Na pewno polecałbym podręczniki takich Panów jak:
−Coexter
−Birkhoff
−Moise
−Euklides
31 sie 19:42
chichi:
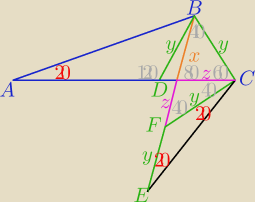
ΔBCE ≡ ΔBDA (cecha b−k−b) → |∡BAC| = 20
o 
31 sie 20:03
chichi:
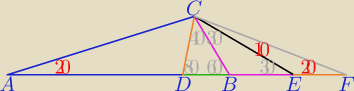
ΔCFD − równoramamienny ∧ ΔAFC − równoramienny → |∡BAC| = 20
o 
31 sie 20:09
chichi:
Trochę spóźnione, ale nie miałem jakoś czasu

31 sie 20:10
Maja: Dlaczego w ostatnim sposobie CDF jest równoramienny?
21 paź 22:31
ajj:
kąty trójkąta CDF : 80o,80o, 20o
czyli Δ CDF równoramienny |DF|=|CF|
21 paź 22:36
maja: Dobrze, a dlaczego właśnie po odłożeniu odcinka EF mamy tam 20 stopni?
23 paź 15:06
chichi:
naturalnie, przedłużam do tego momentu, aż powstanie tam 20
o, aby CDF byl rownoramienny

23 paź 17:08
maja: Ok, gdzieś się zakręciłam, a to takie proste.
Dzięki
23 paź 19:08
maja: Jednak nadal nie rozumiem, przedłużam żeby było 20 stopni, to wiem.
Ale dlaczego wtedy na dole jest pomarańczowy odcinek?
26 paź 11:51
Mariusz:
Przyznasz Maju że te szkolne metody są o wiele łatwiejsze
Trzeba było się trochę pobawić aby wynik uprościć ale upraszczanie nie było trudne
26 paź 18:19
Mila:
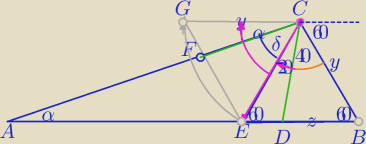
Obrót ΔCEB wokół punktu C o kąt 60
o.
26 paź 20:08
 Wiedzac ze AC=x+y+z, DB=z, CD=x, CB=y oraz ∡DCB=40, ∡BDC=80 i ∡CBD=60 wyznacz ∡BAC.
Wiedzac ze AC=x+y+z, DB=z, CD=x, CB=y oraz ∡DCB=40, ∡BDC=80 i ∡CBD=60 wyznacz ∡BAC.

 ?
?


 P. S.
Jutro wstawię oba rozwiązania i odpowiem na Twoje pytanie w poprzednim wątku, dobranoc
P. S.
Jutro wstawię oba rozwiązania i odpowiem na Twoje pytanie w poprzednim wątku, dobranoc



 ΔBCE ≡ ΔBDA (cecha b−k−b) → |∡BAC| = 20o
ΔBCE ≡ ΔBDA (cecha b−k−b) → |∡BAC| = 20o 
 ΔCFD − równoramamienny ∧ ΔAFC − równoramienny → |∡BAC| = 20o
ΔCFD − równoramamienny ∧ ΔAFC − równoramienny → |∡BAC| = 20o 


 Obrót ΔCEB wokół punktu C o kąt 60o.
Obrót ΔCEB wokół punktu C o kąt 60o.