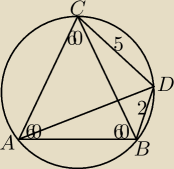
Grześ: Trójkąt ABC jest równoboczny. Długości odcinków CD oraz BD są równe odpowiednio 5 i 2. Wyznacz długość AD.

mat: kąt CDB ma 120 stopni, czemu? wyznacz długość boku CB np z twierdzenia cosinusów wyznacz kąt CBD (też może być z tw cosinusów) na koncu wystarczy roważyc trójkąt ADB i znów tw. cosinusów zapewne da sie prosciej...

chichi: W sensie jakby, what's the matter? Patrząc na to nasuwają się z minimum 3 rozwiązania. Znasz własności czworokąta wpisanego w okrąg?

chichi: "wyznacz kąt CBD (też może być z tw cosinusów)" Do czego przyda się nam ten kąt?

Mila: 1) |BC|²=5²+2²−2*5*2 *cos(120^o) 2) Poproś Ptolemesza o pomoc i gotowe.

chichi: 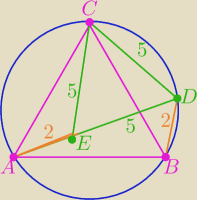(I sposób) ΔACE ≡ ΔBCD ⇒ |AE| = |BD| = 2 ⇒ |AD| = 7 (II sposób) Teorema de Chadu: |AD| = 5+2 = 7

mat: @chichi, żeby wiedzieć potem jaki jest kąt ABD

mat: fajne rozwiązanie chichi!

chichi: "@chichi, żeby wiedzieć potem jaki jest kąt ABD" Aż tak chciałeś, no ok też jakiś sposób, ale jak sam zauważyłeś zbyt długi "fajne rozwiązanie chichi!" Dzięki, ale które?

Grześ: Dziekuje bardzo za rozwiazania, otrzymalem taki sam wynik. Zaraz wstawie kolejne zadanie, do ktorego niestety nie mam pomyslu. Bo to zadanie zrobilem sam ale chcialem sprawdzic czy dobrze je wykonalem.

Mariusz: No tak ale skąd wiesz że te trójkąty są przystające Na pomysł na rozwiązanie który zaproponował mat łatwiej wpaść

ciekawy : Chichi co studiujesz? Masz sporą wiedzę na temat geometrii

Mariusz: Na studiach mu się ona raczej nie przyda

Mariusz: Na studiach to raczej Algebra I rachunek wektorowy (m. in. iloczyn skalarny,wektorowy,liniowa niezależno0ść wektorów, rozkład wektora na składowe) liczby zespolone (tutaj trochę geometrii może jednak być bo interpretacją geometryczną zespolonych jest płaszczyzna ) (postać ogólna ,postać trygonometryczna,działania na liczbach zespolonych) wielomiany w tym twierdzenie że każdy wielomian stopnia większego od zera ma co najmniej jeden pierwiastek zespolony rachunek macierzowy (definicja macierzy , dodawanie , mnożenie , wyznacznik macierzy −metoda permutacyjna obliczania wyznacznika , rozwinięcie Laplace eliminacja Gaußa, twierdzenie Kroneckera−Capellego pozwalające stwierdzić czy układ równań ma rozwiązanie , rozwiązywanie układów równań liniowych , wymiar przestrzeni liniowej, jądro i obraz przekształcenia liniowego , podobieństwo macierzy ,wartości i wektory własne, jakieś rozkłady macierzy np z eliminacją Gaußa związany jest rozkład LU a z wartościami i wektorami własnymi związana jest diagonalizacja i rozkład Jordana) Masz też takie terminy jak grupa , pierścień , ciało @ciekawy to czy będziesz miał więcej zależy od tego na jakie studia pójdziesz np na studiach informatycznych raczej nie będziesz miał więcej algebry niż tutaj podałem Analiza I Tutaj masz przypomnienie definicji funkcji oraz pewnych wiadomości o funkcjach takich jak różnowartościowość , złożenie funkcji , funkcja odwrotna , funkcje elementarne a dalej to ciągi funkcja z N w R granice definicja Heinego i Cauchyego, arytmetyka granic , ciągłość funkcji szeregi granica ciągu sum częściowych warunek konieczny zbieżności kryteria zbieżności takie jak kryterium porównawcze , d'Alemberta i Cauchyego pochodna granica ilorazu różnicowego interpretacja geometryczna i fizyczna współczynnik kierunkowy stycznej, prędkość chwilowa wyprowadzenie wzorów i pochodnych funkcji elementarnych monotoniczność , ekstrema lokalne i globalne zastosowanie pochodnej do liczenia granic − reguła de L'Hospitala druga pochodna wklęsłość/wypukłość funkcji oraz punkty przegięcia przebieg zmienności funkcji Całki podział odcinka [a ,b] granica sumy pól prostokątów o podstawie Δx_i i wysokości f(ξ) gdzie ξ ∊ [x_i,x_i+1] przy max(Δx_i,i=1..n) dążącym do zera Jeżeli dla każdego podziału odcinka granica ta istnieje i jest równa (niezależnie od wyboru podziału przedziału) to granica ta jest całce oznaczonej z f(x) na przedziale [a,b] Uzmiennienie jednego z krańców przedziału i definicja funkcji pierwotnej Twierdzenie że każda funkcja ciągła posiada funkcję pierwotną (co nie znaczy że łatwo ją obliczyć ani nawet że jest ona funkcją ) Pochodna funkcji pierwotnej to funkcja podcałkowa Wynika stąd że funkcje pierwotne mogą się różnić co najwyżej o stałą Całki podstawowych funkcji elementarnych właśnie z powyższej własności funkcji pierwotnej no i z wcześniej stworzonej tabelki pochodnych Podstawowe metody całkowania Liniowość całki (wynika z liniowości pochodnej) Całkowanie przez części (aby wyprowadzić wzór na całkowanie przez części całkujesz obustronnie wzór na pochodną iloczynu , dochodzi jeszcze liniowość całki i wyżej wspomniana własność funkcji pierwotnej) tutaj jako przykład zastosowania całkowania przez części można dać wyprowadzenie kilku przydatnych wzorów redukcyjnych Całkowanie przez zamianę zmiennych (pot przez podstawienie) (aby wyprowadzić wzór na całkowanie przez zamianę zmiennych korzystasz ze wzoru na pochodną złożenia funkcji) Całkowanie funkcji wymiernych Każdy wielomian posiada rozkład na czynniki liniowe lub kwadratowe o ujemnym wyróżniku (co nie oznacza że łatwo taki rozkład znaleźć) Ułamki proste

	A		Bx+C
Ułamki postaci		oraz
	(x−a)k		(x2+px+q)m

	A
Całkę z ułamka prostego		policzymy od razu
	(x−a)k

	Bx+C
natomiast jeśli chodzi o całkę		to
	(x2+px+q)m

rozbijamy ją na sumę dwóch całek

B		2x+p		Bp		1
	∫		dx+(C−		)∫		dx
2		(x2+px+q)m		2		(x2+px+q)m

W pierwszej całce stosujemy podstawienie x²+px+q = t W drugiej całce trójmian kwadratowy w mianowniku sprowadzamy do postaci kanonicznej

	Bp		1
(C−		)∫		dx
	2		p   p2   ((x+ )2+q− )m   2   4

	p		p2
a następnie stosujesz podstawienie (x+		)2=(q−		)t2
	2		4

	1
a do całki ∫		dt stosujesz wyprowadzony przy okazji
	(t2+1)m

całkowania przez części wzór redukcyjny Jeżeli stopień licznika jest większy niż stopień mianownika to wykonujesz dzielenie wielomianów Funkcję wymierną właściwą (w której stopień licznika jest mniejszy od stopnia mianownika) możesz rozłożyć na sumę skończonej liczby ułamków prostych

L(x)		A1		A2		Ak
	=		+		+...+
(x−a)k(x2+px+q)m		x−a		(x−a)2		(x−a)k

	B1x+C1		B2x+C2		Bmx+Cm
+		+		+..+
	x2+px+q		(x2+px+q)2		x2+px+q)m

i dla każdego czynnika w mianowniku tak rozkładasz Po zapisaniu prognozowanego rozkładu na sumę ułamków prostych sprowadzasz ułamki do wspólnego mianownika i po porównaniu współczynników wielomianów w licznikach dostajesz układ równań liniowych do rozwiązania Jest jeszcze sposób Ostrogradskiego na wydzielenie części wymiernej całki co pozwoli wyeliminować z rozkładu na sumę ułamków prostych przypadek wielokrotnych pierwiastków mianownika Jak widzisz liniowość całki pozwala uprościć liczenie całek z funkcji wymiernych Całkowanie funkcyj które da się sprowadzić do całkowania funkcyj wymiernych Całki postaci ∫R(x,√ax²+bx+c)dx Tutaj masz podstawienia Eulera √ax²+bx+c=t±√ax a > 0 (znak możesz sobie wybrać) (wyznaczasz x jako funkcję zmiennej t , różniczkujesz x(t), wyznaczasz pierwiastek jako funkcję zmiennej t i wstawiasz do całki) √ax²+bx+c = xt ± √c c > 0 (znak możesz sobie wybrać) (wyznaczasz x jako funkcję zmiennej t , różniczkujesz x(t), wyznaczasz pierwiastek jako funkcję zmiennej t i wstawiasz do całki) √ax²+bx+c = (x−x₁)t , b²−4ac > 0 (tutaj możesz sobie pierwiastek wybrać) (wyznaczasz x jako funkcję zmiennej t , różniczkujesz x(t), wyznaczasz pierwiastek jako funkcję zmiennej t i wstawiasz do całki) Całka z różniczki dwumiennej Całka postaci ∫x^m(a+bxⁿ)^pdx , gdzie m,n,p ∊ ℚ Jest wyrażona za pomocą skończonej liczby funkcyj elementarnych tylko w trzech przypadkach 1. p ∊ ℤ (tutaj nie potrzeba podstawienia choć jeśli chcemy całkować funkcję wymierną to wtedy podstawiamy x=t^s gdzie s=NWW(mianownik m,mianownik n))

	m+1
2.		∊ ℤ
	n

t^s =(a+bxⁿ) , gdzie s = mianownik p

	m+1
3.		+ p ∊ ℤ
	n

	a+bxn
ts =		, gdzie s = mianownik p
	xn

Całkowanie funkcji postaci R(cos(x),sin(x))dx Wiemy że cos²(x)+sin²(x)=1 , można to wykazać w podobny sposób co twierdzenie Pitagorasa Wcześniej wspominaliśmy podstawienia Eulera można się nimi pobawić aby zaproponować podstawienie dla całek postaci ∫R(cos(x),sin(x))dx Np podstawienie cos(x)=(1−sin(x))t sprowadzi całki postaci ∫R(cos(x),sin(x))dx do całek z funkcji wymiernych Dla uproszczenia przyjmijmy że x należy do pierwszej ćwiartki Mamy że cos(x) = √1−sin²(x) Ze wzoru skróconego mnożenia na różnicę kwadratów mamy 1−sin²(x) = (1−sin(x))(1+sin(x)) √1−sin²(x) = (1−sin(x))t Czyż nie przypomina to nam trzeciego podstawienia Eulera Całki postaci ∫R(e^x)dx Tutaj podstawienie samo się narzuca Do tej postaci można sprowadzić całki z hiperbolicusami Po co ta zabawa z całkami nieoznaczonymi ? Otóż mamy twierdzenie Newtona Leibniza o tym że całka oznaczona jest równa różnicy funkcji pierwotnej na krańcach przedziału Metody obliczania całek oznaczonych Liniowość całki (podobnie jak dla całki nieoznaczonej , w przypadku całki oznaczonej mamy jeszcze addytywność względem przedziału całkowania) Całkowanie przez części − tutaj różnica jest taka że można od razu po obliczeniu części wstawić tzw granice całkowania Całkowanie przez zamianę zmiennych Tutaj różnica jest głównie taka że zmieniamy granicę całkowania Aby zamiana zmiennych była możliwa trzeba czasem podzielić przedział całkowania Podczas liczenia całek oznaczonych mogą wystąpić takie sytuacje jak : funkcja podcałkowa jest nieokreślona dla pewnych argumentów należących do przedziału całkowania przedział całkowania jest nieograniczony W pierwszym przypadku korzystamy z addytywności całki względem przedziału całkowania i liczymy granicę Jeśli granica istnieje i jest skończona wtedy jest ona wartością całki oznaczonej Jeśli chodzi o zastosowania całek oznaczonych to Pole pod krzywą Długość krzywej na przedziale Objętość bryły obrotowej Pole powierzchni bryły obrotowej To czy więcej analizy będziesz miał zależy od tego jakie studia wybierzesz np na studiach informatycznych nie powinieneś mieć tego więcej chociaż jeśli wybierzesz studia informatyczne na wydziale fizyki to możesz dostać jeszcze równania różniczkowe czy przekształcenia Fouriera itp Matematyka dyskretna Zbior liczb całkowitych , relacja podzielności , przystawanie modulo, indukcja matematyczna NWD liczb całkowitych (algorytm Euklidesa i rozszerzony algorytm Euklidesa) Obliczanie odwrotności w ciele Z_p Układy kongruencji (chińskie twierdzenie o resztach) NWD wielomianów nad ciałem (mod p) Małe twierdzenie Fermata i jego uogólnienie zwane twierdzeniem Eulera Omówienie zasady działania niektórych algorytmów kryptograficznych jak np szyfr RSA Zasada włączeń i wyłączeń Funkcje tworzące (zwykła dla ciągu jedynek dająca szereg geometryczny i wykładnicza dla ciągu jedynek dająca exponentę) Alternatywą dla zwykłej funkcji tworzącej mogłoby być przekształcenie Z Równania rekurencyjne Grafy To czy będziesz miał więcej zależy jakie studia wybierzesz Np na studiach informatycznych raczej nie będziesz miał tego więcej Logika i teoria mnogości Zbiory , działania na zbiorach (suma , różnica, iloczyn , dopełnienie) kwantyfikatory,relacje negacja , alternatywa , koniunkcja ,implikacja ,równoważność , tabelka prawdy Rachunek zdań i prawa rachunku zdań Algebra Boole

Mariusz: "Twierdzenie że każda funkcja ciągła posiada funkcję pierwotną (co nie znaczy że łatwo ją obliczyć ani nawet że jest ona funkcją )" Tutaj miało być (co nie znaczy że łatwo ją obliczyć ani nawet że jest ona funkcją elementarną)

chichi: @ciekawy matematykę @Mariusz (1) |∡AEC|=120^o (kąt przyległy) (2) |∡CDB|=120^o (bo czworokąt ABDC wpisany w okrąg) (3) |∡CAD|=α=|∡CBD| (kąty wpisane oparte na łuku CD) (4) |∡ACE|=|∡BCD| No to mamy, że owe trójkąty są przystajace z cechy bok−kąt−bok

Mariusz: To rozwiązanie z trójkątami przystającymi całkiem niezłe bo co do tego drugiego to nie każdy zna to twierdzenie Ja od razu po maturze to nawet dostałem się na nauczycielskie studium fizyki i matematyki ale ostatecznie skończyło się na zaocznej informatyce

chichi: A dlaczego zrezygnowałeś ze studium?

Mariusz: To było 21 lat temu i tak na dobrą sprawę to trudno mi powiedzieć bo zrezygnowałem w momencie w którym nie było jeszcze przesądzone że nie dam sobie rady Później skończyło się to problemami ze snem itp a tak w ogóle to teraz uważam że decyzja o zrezygnowaniu z tych studiów była przedwczesna

chichi: Może jeszcze kiedys najdzie Cię ochota i coś postudiujesz choćby zaocznie

Mariusz: ciekawy gdybyś chciał iść na studia informatyczne to możesz przejrzeć takie książki jak B. Kerningham D. M. Ritchie Język ANSI C B Stroustrup Język C++ B Eckel Thinking in (C++ , Java) Niektórzy polecają też S Prata Język (C / C++) szkoła programowania Możesz obejrzeć też D Knuth Sztuka programowania Z polskich autorów to Jurek Grębosz Symfonia C++ już może jest trochę przestarzała ale ma też inne np Opus magnum C++11 Jeżeli chodzi o algorytmy i struktury danych to Cormen Leiserson Rivest Stein Wprowadzenie do algorytmów Wirth Algorytmy + struktury danych = programy Lafore Algorytmy i struktury danych w Javie a z polskich autorów to Banachowski , Diks , Rytter Algorytmy i struktury danych

Mariusz: Jeśli chodzi o C# to zakładając że jesteś użytkownikiem Windowsa możesz zacząć w nim programować bez ściągania dodatkowego oprogramowania a dokumentację C# możesz łatwo i bezpłatnie znaleźć w sieci

ciekawy : Chichi masz geometrię w takim wymiarze na zajęciach? Jaka uczelnia?