nierówność Rita: Dany jest trójkąt w którym kąty BAC=α i ABC=β ( 0<α<β<π) oraz BC=a i CA=b. Wykaż że b²(1−cosα) < a²(1−cosβ).

ite:

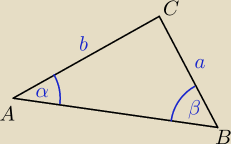
	a		b
z tw. sinusów:		=
	sin α		sin β

a2		b2
	=		podnosimy stronami do kwadratu
sin2α		sin2β

a2		b2
	=		korzystam z jedynki trygonometrycznej
1−cos2α		1−cos2β

a²(1−cos²β)=b²(1−cos²α) a²(1−cos β)(1+cos β)=b²(1−cos α)(1+cos α) teraz skorzystaj z własności funkcji cosinus: w podanym przedziale (0<α<β<π) jest malejąca i spróbuj dokończyć

Rita: No próbuję, czyli to mam pokazać (1−cos β)(1+cos β)> (1−cos α)(1+cos α)

ite: trzeba tylko pokazać, że (1+cos β)<(1+cos α)

wredulus_pospolitus: zauważ, że 0< α < β < π ... tak więc cosα > cosβ (bo w badanym przedziale funkcja f(x) = cosx jest funkcją MALEJĄCĄ )

Rita: ok (1+cos β)<(1+cos α), a co w takim razie z tym (1−cos β)(1+cos β) ? (1−cos α)(1+cos α) ?

ite: wiemy, że (1+cos β)<(1+cos α) oraz 0<α<β<π ⇒ (1+cos β)>0 więc b²(1−cos α)(1+cos β)<b²(1−cos α)(1+cos α) skoro a²(1−cos β)(1+cos β)=b²(1−cos α)(1+cos α) to wstawiam b²(1−cos α)(1+cos β)<b²(1−cos α)(1+cos α)=a²(1−cos β)(1+cos β) upraszczając b²(1−cos α)(1+cos β)<a²(1−cos β)(1+cos β) i b²(1−cos α)<a²(1−cos β)

Rita: Dzięki a ta z kątami taka nierówność β²(1−cosα) > α²(1−cosβ)?

ite: 13:54 to ma być zależność pomiędzy kątami tego samego trójkąta co wcześniej?

Rita: tak zgadza się to jest drugi punkt tego zadania

ite: 0<α<β<π ⇒ wyrażenie 1−cos β przyjmuje jedynie wartości dodatnie Nie przychodzi mi do głowy nic innego niż przekształcenie: β²(1−cos α) > α²(1−cos β)

	β2		α2
do postaci		>
	1−cos β		1−cos α

	α2
i pokazanie, że f(α)=		jest funkcją rosnącą w podanym przedziale.
	1−cos α

Może ktoś wyczaruje szybsze rozwiązanie.

Rita: Jak wykazać że ta funkcja jest rosnąca w podanym przedziale?

Szkolniak: U mnie: α=x oraz β=y b²(1−cos(x))<a²(1−cos(y))

	a
1−cos(x)<(		)2(1−cos(y))
	b

1−cos(x)		a
	<(		)2, bo ⋀(1−cos(y)>0)
1−cos(y)		b

y∊(0;π) Z twierdzenia sinusów:

	a		b		a		sin(x)
		=		→		=
	sin(x)		sin(y)		b		sin(y)

1−cos(x)		a
	<(		)2
1−cos(y)		b

1−cos(x)		sin(x)
	<(		)2
1−cos(y)		sin(y)

1−cos(x)		sin2(x)
	<
1−cos(y)		sin2(y)

(1−cos(x))sin²(y)<(1−cos(y))sin²(x) (1−cos(x))(1−cos²(y))<(1−cos(y))(1−cos²(x)) 1−cos²(y)−cos(x)+cos(x)cos²(y)<1−cos²(x)−cos(y)+cos(y)cos²(x) cos²(x)−cos²(y)+cos(y)−cos(y)cos²(x)−cos(x)+cos(x)cos²(y)<0 (cos(x)−cos(y))(cos(x)+cos(y))+(cos(y)−cos(x))+cos(x)cos(y)(cos(y)−cos(x))<0 (cos(y)−cos(x)(cos(x)+cos(y))−(cos(y)−cos(x))−cos(x)cos(y)(cos(y)−cos(x))>0 (cos(y)−cos(x))((cos(x)+cos(y)−1−cos(x)cos(y))>0 Z tego co wredulus napisał, mamy że cos(y)−cos(x)<0, zatem pozostaje nam do udowodnienia taka nierówność: cos(x)+cos(y)−1−cos(x)cos(y)<0 cos(x)−1+cos(y)−cos(x)cos(y)<0 (cos(x)−1)+cos(y)(1−cos(x))<0 (1−cos(x))−cos(y)(1−cos(x))>0 (1−cos(x)(1−cos(y))>0 Zbiór wartości funkcji f w przedziale (0;π): 1) f(x)=cos(x) −> (−1;1) 2) f(x)=−cos(x) −> (−1;1) 3) f(x)=−cos(x)+1 −> (0;2) + odpowiedni teraz wniosek, może ktoś oceni czy taki dowód byłby ok?

ite: Rita żeby wykazać, że badana funkcja jest rosnąca w podanym przedziale można zbadać znak f.pochodnej. To jest w materiale szkoły średniej.

ite: Szkolniak nie sprawdzałam tych przekształceń (czy próbujesz pobić rekord należący do Mariusza?: ), ale zaczynasz je od tezy.

Szkolniak: @ite Ja sprawdziłem kilka razy i błędu nie widzę, ale może komuś będzie się chciało. Do poziomu Mariusza jeszcze mi daleko także nie ma co porównywać Chociaż zdaje sobie sprawę że dosyć ciężko by się to sprawdzało bo ogrom tam nawiasów, cosinusów i sinusow