Wbrew pozorom nie jest to równanie dwukwadratowe
Enklaar: Jak rozwiązać takie równanie?
x4 + 4x − 1 = 0
Wydaje się proste, ale wbrew pozorom nie jest to równanie dwukwadratowe.
21 sie 09:14
pink: ...(x2+1)2−(√2(x−1))2=(x2+√2 x+1−√2)(x2−√2 x+1+√2)
21 sie 09:30
Enklaar: I co dalej? Próbowałem rozwiązywać oba wyrażenia kwadratowe w nawiasach, ale nie udało mi się
wyliczyć x.
21 sie 10:22
pink: no delta...
jedno jest zawsze dodatnie a drugie
(√2±(4√2−2)1/2)/2
21 sie 10:30
Enklaar: Delta mi wychodzi 2x2 + 4 p{2) − 4
Coś jest nie tak w tych przekształceniach równania wyjściowego. Nic nie kumam.
21 sie 10:39
pink: 2 + 4 p{2) − 4
21 sie 10:51
21 sie 20:22
Mila:
L=x
4+4x−1= x
4+2x
2+1−2x
2+4x−2=
(x
2+1)
2−2*(x
2−2x+1)=(x
2+1)
2−2(x−1)
2⇔
x
4+4x−1=[x
2+1−
√2(x−1)]*[x
2+1+
√2(x−1)]
[x
2+1−
√2(x−1)]=0 lub [x
2+1+
√2(x−1)]=0
x
2+1−
√2x+
√2=0 lub x
2+1+
√2x−
√2=0
x
2−
√2x+
√2+1=0 lub x
2+
√2x+1−
√2=0
Δ=2−4*(
√2+1}<0 brak rozwiązań lub Δ=2−4+4
√2=4
√2−2>0
| | −√2−√4√2−2 | | −√2+√4√2−2 | |
x1= |
| lub x2= |
| |
| | 2 | | 2 | |
21 sie 21:06
Enclaar: Rozwiąż równanie
32−x + 2 * 3x−2 = 613
Jak rozwiązać takie równanie wykładnicze?
21 gru 09:29
I'm back:
3x−2 = 3−(2−x) = 1/32−x
Podstawienie:
t = 32−x
t + 2/t = 10/3
Czyli:
t2 − 10t/3 + 2 = 0
Δt =...
Dorzucasz warunki i rozwiazujesz
21 gru 09:34
chichi:
Jak otrzymałeś takie równanie?

21 gru 10:16
21 gru 10:17
chichi:
Ja widzę dwa razy 10/3, ale Ty chyba masz jakieś moce

21 gru 10:37
I'm back:
Ciiii... Przywidziało Ci się

21 gru 10:40
Enclaar: Nadal nie rozumiem tego rozwiązania.
32−x + 2 * (13)2−x = 193 i dalej jeśli t = 32−x to mamy równanie
t2 − 19t3 + 2 = 0 i wychodzą jakieś kosmiczne pierwiastki.
Powyższa metoda liczenia tego równania jest chyba niepoprawna
Poprawne pierwiastki to x = 3 lub x = 1 − u{log2}{log3), tylko pytanie jak do tego dojść.
21 gru 13:19
chichi:
3t
2−19t+6 = 0 ⇔
(3t−1)(t−6) = 0 ⇔
Jak te rozwiązania są 'kosmiczne' to jakie są te 'normalne'?

21 gru 13:24
ICSP: | | 3 | |
x = 2 − log3(6) = log3( |
| ) = 1 − log3(2) (wybierz dowolną z tych 3 postaci) |
| | 2 | |
no i oczywiście
x = 3
21 gru 13:44
Enclaar: Bardzo dziękuję za pomoc. Oczywiście wszystko się zgadza. Źle policzyłem równanie kwadratowe.
21 gru 19:58
Enclaar: Rozwiązać równanie
32 − √x = {√92−2√x + 2 (wyrażenie {9}2−2√x jest pod pierwiastkiem
kwadratowym).
Proszę o podpowiedź jak to rozwiązać
22 gru 08:35
chichi:
3
2−√x =
√92−2√x+2 ⇔
3
2*3
−√x =
√(91−√x)2+2 ⇔
9*3
−√x = 9
1−√x+2 ⇔
9*3
−√x = 9*(3
−√x)
2+2, t = 3
−√x ⇔
| | 1 | | 2 | |
9t = 9t2+2 ⇔ (3t−1)(3t−2) = 0 ⇔ t ∊ { |
| , |
| } |
| | 3 | | 3 | |
3
−√x = 3
−1 ⇔ −
√x = −1 ⇔ x = 1
3
−√x = 2*3
−1 ⇔ −
√x = log
3(2)−1 ⇔ x = (1−log
3(2))
2
22 gru 09:19
Enclaar: Dziękuję chichi za super rozwiązanie.
Czy drugie rozwiązanie tego równania może być
x = {log2*32−{log2}3 ?
22 gru 10:52
chichi:
A gdzie jest argument tych logarytmów, zapisz to porządnie

22 gru 11:54
Enclaar: Mam problem z rozwiązaniem następującego równania wykładniczego z różnymi podstawami.
5*4x − 7*10x + 2*25x = 0
Prosiłbym o podpowiedź.
26 gru 18:22
ABC: | | 2 | | 5 | |
standard , podziel obie strony przez 10x i niewiadoma pomocnicza bo |
| i |
| |
| | 5 | | 2 | |
są odwrotnościami
26 gru 18:34
mat:
(2x−5x)(5*2x−2*5x)=0
x=0 v x= 1
26 gru 19:15
Enclaar: Jak rozwiązać takie równanie?
log√7x+5 +12log(2x+7) = 1 + log4,5
27 gru 11:14
janek191:
x = 10
27 gru 11:40
janek191:
2 x + 7 > 0 ⇒ x > −3,5
12 log ( 7 x + 5) +
12 log (2 x +7) = 1 + log 4,5 / *2
log[ ( 7 x + 5)*(2 x + 7)] = log 100 + log 20,25
14 x
2 + 49 x + 10 x + 35 = 2025
14 x
2 + 59 x − 1990 = 0
Δ = 114 921
√Δ = 339
| | −59 − 339 | | 6 | |
x = |
| = − 14 |
| − odpada |
| | 28 | | 28 | |
lub
=====================
27 gru 11:49
Enclaar: Dziękuję super OK.
27 gru 13:04
Filip:
x4 + 4x − 1 = 0
(x2 + 1)2 − 2x2 + 4x − 2 = 0
(x2 + 1)2 − 2(x2 − 2x + 1) = 0
(x2 + 1)2 − 2(x − 1)2 = 0
(x2 + 1 − √2(x − 1))(x2 + 1 + √2(x − 1)) = 0
27 gru 20:15
Enclaar: Jak rozwiązać takie równanie logarytmiczne;
5logx = 50 − xlog5
Czy tu wystarczy pomnożyć obie strony równania x 10 i zastosować wzór alogax = x ?
2 sty 11:03
ABC: przecież 5logx=xlog5
więc masz y=50−y czyli y=25
2 sty 11:23
Enclaar: Nie za bardzo kumam. To w takim razie ile wynosi x?
2 sty 12:15
ABC: 5logx=25
log x=2
x=100
2 sty 13:12
Enclaar: Dziękuję. OK
2 sty 14:34
Enclaar: Ściany boczne ostrosłupa prawidłowego trójkątnego są trójkątami prostokątnymi równoramiennymi.
Oblicz objętość tego ostrosłupa, jeśli krawędź podstawy ma długość 6 cm.
Obliczyłem pole podstawy tego ostrosłupa które wynosi 9√3 ale nie wiem jak wyliczyć wysokość
tego ostrosłupa.
5 sty 16:55
a7:
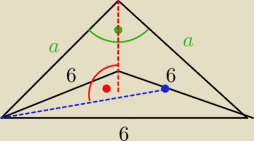
a
√2=6 ⇒a=3
√2
h=3
√3 2/3*h=2
√3
V=1/3p
p*H=1/3*9
√3*
√6=9
√2 (cm
3)
5 sty 17:02
Klara:
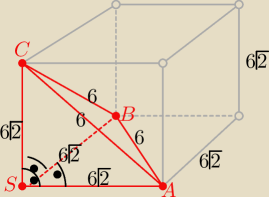
Ostrosłup taki jest narożem sześcianu o krawędzi 6
√2
| | 1 | | 1 | |
Vo= |
| Vszescianu= |
| 216*2√2= 72√2 |
| | 6 | | 6 | |
lub tak:
P
p=P(ABS)=36, H=|CS|=6
√2
V(ABCS)= 12*6
√2=72
√2
5 sty 17:33
a7: jakby ten sześcian miał krawędź 6√2 (powinno być 3√2) to przekątna (krawędź podstawy
ostrosłupa) byłaby 12
5 sty 17:36
a7: u mnie błąd w obliczeniu V=1/3*9√3√6=27√2
5 sty 17:38
Klara:
Achhhhhhhh sorrry
szescian ma krawędź długości 3√2 oczywiście
V= 9√2
Dzięki a7 za poprawkę
5 sty 17:39
a7: a nie chyba jednak było u mnie dobrze, już się zgubiłam ....
5 sty 17:39
a7: a no teraz się zgadza dzięki
Klara 
Pozdro
5 sty 17:40
Enclaar: Bardzo dziękuję za wyjaśnienia i pozdrawiam.
5 sty 18:54
Enclaar: Kąt nachylenia krawędzi bocznej ostrosłupa prawidłowego sześciokątnego do podstawy wynosi
60 stopni.Podaj miarę kąta nachylenia ściany bocznej tego ostrosłupa do podstawy,
jeśli krawędź podstawy ma miarę 6 cm.
Proszę o pomoc w rozwiązaniu tego zadania.
6 sty 13:07
Klara:
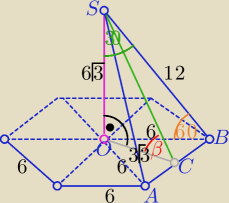
|OS|=H=6
√3
|OC|=3
√3
to w ΔSOC : tgβ=2 ⇒β=... odczytaj z tablic
6 sty 17:29
Enclaar: Dziękuję za pomoc.
7 sty 08:36
Enclaar: Sześcian ABCDEFGH przecięto płaszczyzną przechodzącą przez środki 2 sąsiednich
krawędzi podstawy (punkty K i L) i wierzchołek G. Oblicz objętość
i pole powierzchni całkowitej powstałego ostrosłupa trójkątnego CKLG jeśli krawędź
podstawy sześcianu ma długość 4 cm.
Jak obliczyć pole podstawy ostrosłupa KCL i jego pole powierzchni bocznej?
8 sty 10:24
Mila:
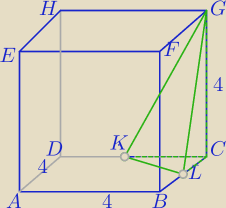
Czy tak obrałeś K i L?
8 sty 15:51
a7: KC=CL=2
PKLC=1/2*2*2=2
V=1/3*Pp*H=1/3*2*4=8/3
PGLC=PGKC=1/2*2*4=4
PGKL=1/2*|KL|*hKL=1/2*2√2*3√2=6
hKL=√GL2−(KL/2)2=√20−2=√18=3√2 GL=√42+22=2√5
Pc=2+4+4+6=16
8 sty 16:05
Mila:
Witaj
A7 
Można też na innych krawędziach obrać Punkty K i L .
8 sty 16:54
a7: Witaj
Mila jasne

8 sty 17:09
Mila:
Nie wiadomo, jaka dokładnie treść

8 sty 17:17
Enclaar: Dziękuję Mila. Punkty K i L miały być dobrane właśnie tak jak na rysunku.
Rozwiązanie super. Jeszcze raz dziękuję.
8 sty 17:25
a7: a no tak jakby płaszczyzna przechodziła przez AD i AB to wynik byłby inny
8 sty 17:36
a7: nie no jednak nie rozuemim 16:54 przecież tylko przez te krawędzie co narysowałaś Milu
powstanie ostrosłup inaczej będzie inna figura
8 sty 17:40
Mila:
Enclaar, z następnymi zadaniami załóż nowy wątek,
bo teraz trzeba długo przewijać stronkę

8 sty 20:28
Enclaar: Mam problem z rozwiązaniem takiego równania logarytmicznego
(2x√x)logx * xlog√x = 21+log√x
Proszę o pomoc.
5 lut 17:07
mat:
x=100
5 lut 17:38
Enclaar: To wynik. ale jak do tego dojść, jak to wyliczyć?
5 lut 17:58
Eta:
x>0
| 2 | | 2 | |
| *√x= |
| j xlog√x= √xlogx |
| x | | √x | |
| | 2 | | 2 | |
to ( |
| )logx*(√x)logx = ( |
| *√x)logx= 2logx |
| | √x | | √x | |
i mamy: 2
logx=2
1+log√x
| | x | |
logx=1+log√x ⇒log( |
| )=1 ⇒ log√x=1 ⇒ √x=10 |
| | √x | |
x= 100
5 lut 18:26
Enclaar: Dziękuję za pomoc. Wynik OK.
5 lut 19:52
Min. Edukacji: Enclaar ty nic nie kumasz?
Nowy Wątek w nowym poście to nie papirus!
5 lut 22:55
Enclaar: Jak rozwiązać
Ile dzielników ma liczba 2 x 3 x 5 x 7 x 11 x 13 x 17 x 19 ?
11 cze 10:54
dzielnik:
n = p1k1 * p2k2 * p3k3 * ... * pmkm
p1, p2, p3, ... , pm − liczby pierwsze
k1, k2, k3, ... , km − naturalne wykładniki ≥ 1
Liczba dzielników liczby naturalnej n jest równa (k1+1)*(k2+1)*(k3+1)* ... *(km+1)
np. liczba dzielników liczby 360 = 23*32*51 wynosi (3+1)*(2+1)*(1+1) = 4*3*2 = 24
11 cze 14:45
ite:
10:54 to nie będzie ilość podzbiorów zbioru ośmioelementowego? Bo tyle jest tych pierwszych
czynników.
11 cze 14:49
Szkolniak: ite, ja się zgadzam, bo przykładowo liczba 23*74*116 ma (3+1)*(4+1)*(6+1) dzielników.
11 cze 14:57
Enclaar: To ile w końcu jest tych dzielników podanej liczby?
To jest iloczyn ośmiu liczb pierwszych w których wykładnikiem naturalnym jest 1.
Proszę o rozwiązanie.
11 cze 17:34
ite:
Oba zaproponowane rozwiązania dają ten sam wynik, po prostu opierają się na innych
spostrzeżeniach (zaczęłam pisać, nie widząc wcześniejszej odpowiedzi).
To, co napisałeś 17:34, wykorzystaj we wzorze podanym przez dzielnik.
11 cze 18:13






 a√2=6 ⇒a=3√2
h=3√3 2/3*h=2√3
a√2=6 ⇒a=3√2
h=3√3 2/3*h=2√3
 Ostrosłup taki jest narożem sześcianu o krawędzi 6√2
Ostrosłup taki jest narożem sześcianu o krawędzi 6√2
 Pozdro
Pozdro
 |OS|=H=6√3
|OC|=3√3
to w ΔSOC : tgβ=2 ⇒β=... odczytaj z tablic
|OS|=H=6√3
|OC|=3√3
to w ΔSOC : tgβ=2 ⇒β=... odczytaj z tablic
 Czy tak obrałeś K i L?
Czy tak obrałeś K i L?
 Można też na innych krawędziach obrać Punkty K i L .
Można też na innych krawędziach obrać Punkty K i L .


