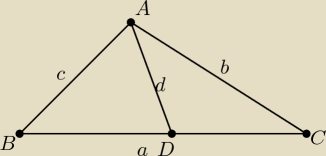
zadanie ambitniejsze :P bardzo prosze o pomoc. Ergo :): 1) W trojkacie ABC mamy dane |AB|=10cm , |AC|=20cm i |<BAC|=120^o. Wyznacz dlugosc srodkowej AD oto moje obliczenia spedzilem dosyc sporo czasu na rozwiazaniem tego zadania i niestety nieudalo sie obliczam |BC| : |BC|=a |AB|=c |AC|=b a²=c²+b² −2a*b*cos120^o

	1
a2=102+202−2*10*20*(−		)
	2

a²=100+400+200 a²=700 a=10√7 |<BDA|=α i |<ADC|=180^o−α i dalej twierdzenie cosinusow? czy zla droge obieram?

Basia: b=20 c=10 a=10√7 BD=CD=5√7 β+γ=60 γ=60−β d²=(a/2)²+c²−2*(a/2)*c*cosβ d²=(a/2)²+b²−2(a/2)*b*cos(60−β) (a/2)²+c²−ac*cosβ=(a/2)²+b²−ab*cos(60−β) 100−100√7*cosβ=400−200√7*[cos60*cosβ−sin60*sinβ]

	cosβ		√3sinβ
100−100√7*cosβ=400−200√7*[		−		]
	2		2

100−100√7*cosβ=400−100√7*(cosβ−sinβ) 100√7√3sinβ=300

	3
sinβ=
	√21

z wzoru sin^β+cos²β=1

	√12		√3*4		2
wylicz cosβ=		=		=
	√21		√3*7		√7

podstaw do d²=(a/2)²+c²−2*(a/2)*c*cosβ i gotowe

Basia: sprawdź ten cosβ, bo liczyłam w pamięci

Ergo :): dziekuje bardzo juz sprawdzam

fletch: coś nie pasuje... cos(α−β) = cosαcosβ+sinαsinβ

rafcio: A i tak Basia wyszła na swoje niezależnie od tego błędu 100−100√7*cosβ=400−200√7*[cos60*cosβ+sin60*sinβ] −300−100√7*cosβ=−100√7*(cosβ+√3sinβ) 300=100√7(−cosβ + cosβ + √3sinβ) 100√7√3sinβ=300 i dalej to samo co przedtem napisała koleżanka