proszę o rozwiązanie anna: trójkąt ABC jest trójkątem równobocznym o boku a wykaż że łuk okręgu wpisanego w ten trójkąt zawarty między dwoma kolejnymi punktami styczności tego okręgu z bokami trójkąta ma długość większą niż 60% a

kerajs:

	1		1		a√3
Długość tego łuku to:		(2π(		(		)))
	3		3		2

chichi:

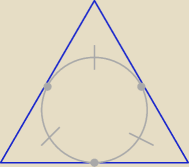
1		a√3		3		π√3		3
	*2π*		>		a ⇒		>		□
3		6		5		9		5

anna: czy można prosić o dokładniejsze wyjaśnienie

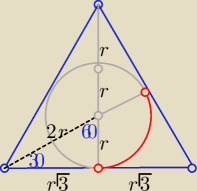
blabla: a=2r√3

2		3
	πr >		*2r√3 / : 2r
3		5

	π		3√3
		>
	3		5

5π > 9√3 15,7> 15,57

a7: promień okręgu w pisanego w trójkąt równoboczny to jedna trzecia jego wysokości h=a√3/2 r=1/3*a√3/2=a√3/6 obwód okręgu to 2πr podstawiamy za r a√3/6 i łuk to jedna trzecia tego obwodu czyli 1/3π*2a√36=πa√3/9 teraz musimy sprawdzić czy π√3/9 jest większe niż 6/10 π√3/9≈0,604582 >0,6 c.n.w

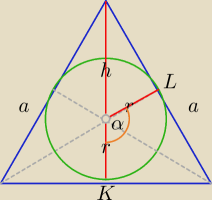
Mila: 1) α=2*60^o

	α		απ
ł=		*2π*r=		*r
	360o		180o

	120		2
ł=		*πr=		π*r
	180		3

	1		1		a√3		a√3
2) r=		h=		*		=
	3		3		2		6

	2		a√3
ł=		π*		>a*6.28*1.73/18≈0.6042a
	3		6