19 sie 14:19
wredulus_pospolitus:
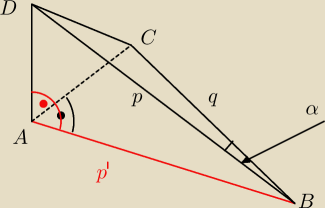
niech ω będzie płaszczyzną zawierającą podstawę tegoż czworościanu.
Masz wykazać, że α = 60
o wiedząc, że:
∡ABD = 45
o
ΔABD to trójkąt prostokątny równoramienny (patrz kąt ABD)
∡ABC = 45
o
ΔABC to trójkąt prostokątny równoramienny (patrz kąt ABC)
niech |AB| = x, wtedy:
|AC| = |AB| = x −−> |BC| = x
√2
|AD| = |AB| = x −−−> |DB| = x
√2
zauważ tak, że ΔCAD jest także prostokątny (i równoramienny, ale to już mniejsza z tym)
−−−> |DC| = x
√2
tak więc Δ BCD jest trójkątem równobocznym

stąd ∡CBD = α = 60
o
c.n.w.
19 sie 15:06
uczesie: Dla mnie to było trudne, a tam jest napisane że łatwe
19 sie 15:19
uczesie: Gdzie na twoim rysunku prosta p przebija płaszczyznę w punkcie A?
19 sie 15:40
wredulus_pospolitus:
punktem 'A' z treści zadania jest wierzchołek B (przy robieniu rysunku nie miałem podglądu na
zadanie)
po prostu zmień oznaczenia
19 sie 15:42
uczesie: czumu ΔABD i ΔABC równoramienne?
19 sie 15:50
wredulus_pospolitus:
napisałem −−− patrz kąt ABD i kąt ABC (masz podane, że te kąty wynoszą 45
o 
)
19 sie 15:51
uczesie: ok a czemu ΔCAD prostokątny?
19 sie 15:55
wredulus_pospolitus:
żeby sobie wyobrazić tą sytuację, która jest opisana w zadaniu polecam:
1) bierzesz do ręki długopis
2) stół jest płaszczyzną ω, długopis stawiasz na stole i nachylasz go pod kątem ~45o (prosta
p)
3) część stołu która jest 'pod długopisem' to rzut prostopadły (p')
4) kładziesz na stole drugi długopis pod kątem ~45o do (p') (cienia uniesionego długopisu −−−
zakładając że światło jest nad stołem) ... to jest prosta q
Tak wygląda ten ostrosłup
19 sie 15:56
wredulus_pospolitus:
zrób jak napisałem −−− będzie Ci łatwiej to zauważyć ... niestety ... wiele osób ma problem z
wyobraźnią przestrzenną, dlatego warto (także na maturze) spróbować sobie to pokazać
korzystając z przyborów posiadanych w trakcie rozwiązywania zadania.
Tak naprawdę − zadanie to nie jest trudne, o ile właśnie wpadnie się na to, że te trzy proste
(dwie proste i rzut) tworzą ten czworościan.
Gdyby w zadaniu było podane, że masz czworościan taki jak opisałem, spodziewam się, że nie
miałbyś/miałabyś z tym zadaniem najmniejszego problemu.
19 sie 15:59
uczesie: Ok rzeczywiście trzeba wyobraźni aby zauważyć że CAD jest prosty.
19 sie 16:10
wredulus_pospolitus:
zrobiłeś/−aś tak jak zaproponowałem? Widzisz już ten ostrosłup?
19 sie 16:21
uczesie: tak, dziękuju
19 sie 16:23
 niech ω będzie płaszczyzną zawierającą podstawę tegoż czworościanu.
Masz wykazać, że α = 60o wiedząc, że:
∡ABD = 45o
ΔABD to trójkąt prostokątny równoramienny (patrz kąt ABD)
∡ABC = 45o
ΔABC to trójkąt prostokątny równoramienny (patrz kąt ABC)
niech |AB| = x, wtedy:
|AC| = |AB| = x −−> |BC| = x√2
|AD| = |AB| = x −−−> |DB| = x√2
zauważ tak, że ΔCAD jest także prostokątny (i równoramienny, ale to już mniejsza z tym)
−−−> |DC| = x√2
tak więc Δ BCD jest trójkątem równobocznym
niech ω będzie płaszczyzną zawierającą podstawę tegoż czworościanu.
Masz wykazać, że α = 60o wiedząc, że:
∡ABD = 45o
ΔABD to trójkąt prostokątny równoramienny (patrz kąt ABD)
∡ABC = 45o
ΔABC to trójkąt prostokątny równoramienny (patrz kąt ABC)
niech |AB| = x, wtedy:
|AC| = |AB| = x −−> |BC| = x√2
|AD| = |AB| = x −−−> |DB| = x√2
zauważ tak, że ΔCAD jest także prostokątny (i równoramienny, ale to już mniejsza z tym)
−−−> |DC| = x√2
tak więc Δ BCD jest trójkątem równobocznym  stąd ∡CBD = α = 60o
c.n.w.
stąd ∡CBD = α = 60o
c.n.w.
 )
)