prostopadłścian kamila: Rozważmy prostopadłościan ABCDEFGH z AB=5, BC=4 i BF=6. Niech R oznacza zbiór punktów znajdujących się wewnątrz prostopadłościanu takich że |BF|≤3 i niech S oznacza zbiór punktów znajdujących się wewnątrz takich że |CG|≤3. Niech P oznacza przecięcie R i S, jaka jest objętość P?

ite: Czy na pewno |BF|≤3, skoro BF=6 ? Może |BR|≤3 ?

Darko: Żle objaśniłam, poniżej poprawione Rozważmy prostopadłościan ABCDEFGH z AB=5, BC=4 i BF=6. Niech R oznacza zbiór punktów znajdujących się wewnątrz prostopadłościanu takich że ich odległość od BF jest mniejsza bądź równa 3 i niech S oznacza zbiór punktów znajdujących się wewnątrz takich że ich odległość od CG jest mniejsza bądź równa 3. Niech P oznacza przecięcie R i S, jaka jest objętość P?

ite: A widzisz, jaką figurą jest to przecięcie?

kamila: jakiś prostopadłościan chyba

ite: tutaj widać, zaznaczone są wszystkie punkty przestrzeni odległe od krawędzi BF o 3 lub mniej, do szukanego zbioru należą tylko punkty wewnątrz prostopadłościanu https://www.geogebra.org/3d/u72xauab

kamila: to 1/4 walca, i od CG też bedzie 1/4 walca a cześć wspólna to jaka bedzie?

ite: https://prnt.sc/1qbpnhq Ja bym od obliczonej proporcjonalnie (ale nie 1/4) objętości walca odjęła objętość prostopadłościanu o podstawie będącej trójkątem prostokątnym (ten z czarnymi krawędziami) i otrzymany wynik pomnożyła przez 2.

kamila: Czemu nie 1/4? i ta podstawa trójkata wynosi 2?

ite: Przecięcie R i S to jest ich część wspólna, a nie suma (tak jak chciałaś liczyć 12:21).

kamila: No wiem ale miałam na myśli jeden walec i sześcian, a jak to policzyć w takim razie?

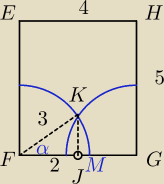
ite: widok "z góry" Pole ΔFKJ to podstawa graniastosłupa, którego objętość trzeba odjąć od części walca o kącie α i łuku KM. Nie wiem, o jaki sześcian chodzi (13:29)?

kamila: Rozumiem ale jak policzyć objętość tej cześci walca http://www.artom.com.pl/Oblicz/walec.jpg

ite:

objętość części wyciętej		α
	=
objętość całego walca		2π