ostrosłup 123: Wszystkie ściany trójkątnego ostrosłupa są równoramiennymi trójkątami prostokątnymi, z wyjątkiem podstawy, która jest trójkątem równobocznym. Wysokość ostrosłupa wynosi H. Oblicz jego objetość.

wredulus_pospolitus: Masz 4 przypadki: 1) wszystkie trzy kąty proste są u podstawy 2) dwa kąty proste u podstawy, jeden przy wierzchołku 3) jeden kąt prosty u podstawy, dwa przy wierzchołku 4) trzy kąty proste u wierzchołka sprawdzasz, które z tych przypadków mogą zaistnieć gdy podstawa to trójkąt równoboczny, a ściany boczne to trójkąty równoramienne prostokątne (podpowiedź − jeden przypadek tylko wchodzi w grę) I liczysz

123: trzy kąty proste u wierzchołka

wredulus_pospolitus: da. jednak pozostałe możliwości trzeba podać i pokazać(wykazać), że nie mają one racji bytu przy takich danych zadania.

123: Chyba w tych pozostałych przypadkach nie da się tego narysować, aby trójkąt równoboczny był w podstawie. Czyli to jest ostrosłup foremny?

wredulus_pospolitus: 1) nie da się −−− masz jednak to wykazać 2) nie czworościan foremny (ostrosłup foremny −−− bo on ma wszystkie ściany jako trójkąty równoboczne) tylko ostrosłup prawidłowy

chichi: Ostrosłup prawidłowy = ostrosłup foremny

chichi: Skąd taki wniosek wredulusie?

123: Nie wiem jak np wykazać wszystkie trzy kąty proste są u podstawy nie mogą być

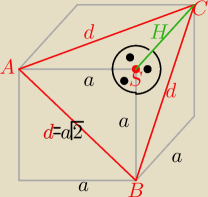
blabla: Taki ostrosłup to naroże sześcianu H=a

	1		H2
V=		*		*H
	3		2

	H3
V=
	6

=========

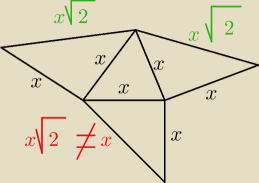
wredulus_pospolitus: @chichi −−− nie wiem skąd @123 −−− zaczynając od tego, że taki ostrosłup nie istnieje (nie 'zamknie się' ) ale pomijając to, zrób sobie siatkę i popatrz jakie będą miały długości krawędzie boczne (i nie czepiać się mojego trójkąta 'równobocznego' )