szescian amelka: Niech A B C D A' B' C' D' będzie sześcianem o długości krawędzi 1. Na krawędzi BC znajduje się punkt J tak że 3|CJ| = |BC|, na krawędzi A' D' znajduje się punkt M tak ze 3|A'M| = |A' D'|. Wyznacz pole trójkąta MDJ.

Mila: Masz odpowiedź?

amelka: Niestety nie mam

amelka: Mam jednak √7/18

Szkolniak:

	√13		√10		√19
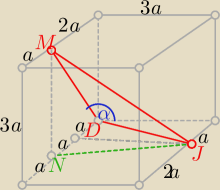
Mi boki trójkąta wyszły równe		,		oraz		, a Tobie @Mila?
	3		3		3

chichi: Rozważmy sześcian o wierzchołkach: A=(0,0,0) B=(1,0,0) C=(1,1,0) D=(0,1,0) A'=(0,0,1) B'=(1,0,1) C'=(1,1,1) D'=(0,1,1) Wówczas: M=(0, 1/3, 1) ∧ J=(1, 2/3, 0) vec(MJ)=[1, 1/3, −1] ∧ vec(MD)=[0, 2/3, −1] | i j k | vec(MJ) x vec(MD) = |1 1/3 −1| = (2/3)k + (1/3)i + j = [1/3, 1, 2/3] |0 2/3 −1|

	1		√14
PΔMDJ =		√1/9+1+4/9 =
	2		6

blabla: Dobrze Szkolniak |MD|²=13a² , |DJ|²=10a² , |MJ|²=19a²

	2
cos(MDJ)=cosα=
	√130

	126
sin2α=
	130

	1		1
P2=		*13a2*10a2*sin2 , 3a=1 to a2=
	4		9

	126		7
P2=		=
	18*18		18

P=√7/18

chichi:

	√10		√13		√19
Z Pitagorasa boki trójkąta mamy:		,		,		.
	3		3		3

	10		13		19		2√247		11
Z tw. Carnota mamy, że:		=		+		−		cosα ⇒ cosα=
	9		9		9		9		√247

	√126
Z jedynki tryg. mamy: sinα=√1−11/√247=
	√247

	1		√126		√14
PΔMDJ=		*√13*√19*		=
	2		√247		6

chichi: O, już ktoś wyprzedził

chichi: W polu zgubiłem 3 w mianownikach pod pierwiastkami

blabla:

Mila: Szkolniak Tak też mam.