funkcje wymierne ciufcia: Wykres funkcji g jest symetryczny względem prostej x=−1 do wykresu funkcji:

	10 − 2x
f(x) =		. Rozwiąż nierówność f(x)−g(x)>=0
	x − 2

Niestety nie do końca rozumiem jak zrobić to zadanie, więc prosiłbym o wytłumaczenie Z góry dziękuję.

chichi:

	10−2x		−2(x−2)+6		6
f(x) =		=		=		−2 teraz już chyba pójdzie co?
	x−2		x−2		x−2

ciufcia: No właśnie to znalazłem, ale niestety nie rozumiem co dalej haha

ciufcia: albo bardziej obliczyłem a nie znalazłem

ciufcia: A wogóle wynik końcowy to x ∈ (−4; −1> u (2;niesk)

chichi: P=(x,y) −−−− S=(−2,y) −−−− P'=(x',y)

x+x'
	= −2 ⇒ x = −4−x'
2

	6		6		14+2x
g(x) =		−2 ⇒ g(x) = −		−2 = −
	−4−x'		x+4		x+4

	10−2x		14+2x
f(x)−g(x) ≥ 0 ⇔		+		≥ 0
	x−2		x+4

(10−2x)(x−2)+(14+2x)(x+4)
	≥ 0
(x−2)(x+4)

12(x+1)(x−2)(x+4) ≥ 0 ⇒ x ∊ (−4,−1] ∪ (2, +∞)

chichi: Tam w przedostatniej linijce zamieniłem nawiasy przy przepisywaniu, licznik winien być postaci: (10−2x)(x+4)+(14+2x)(x−2) dalsze rozumowanie jest ok

ciufcia: WOOOO Dobra dziękuję bardzo

ciufcia: Teraz już rozumiem, ale ta społeczność na tym forum jest pomocna

chichi: Nie ma za co

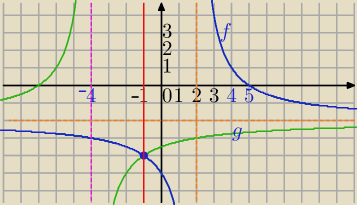
Mila: 1) Symetria względem prostej x=m Obrazem punktu P=(x,y) jest punkt P'(x',y') taki, że x'=2m−x y'=y 2) Symetria względem prostej x=−1 x'=2*(−1)−x y'=y ====== x=−x'−2 y=y' 2)

	10−2x
y=		, x≠2
	x−2

	10−2*(−x'−2)		2x'+14
y'=		=
	−x'−2−2		−(x'+4)

	2x+14
3) g(x)=
	−(x+4)

chichi: @Mila zobacz co się u mnie wydarzyło, dokonywałem symetrii względem prostej x=−2, ale przy wyznaczaniu g(x) nie odjąłem 2 w mianowniku i ostatecznie wyszedł mi wzór funkcji g, jak dla symetrii względem prostej x=−1

ciufcia: Ooo Dziękuję za kolejną odpowiedź, przeanalizuje sobie i będę wiedział na przyszłość. Dziękuję bardzo

ciufcia: @chichi faktycznie nie zauważyłem tego, dzięki już wiem więcej

Mila: ciufcia przekształć f(x) z postaci kanonicznej, mniej liczenia i okazji do pomyłek. chichi ładnie Ci się udało.

ciufcia: jasne dzieki